题目内容
11.求函数y=x-1+$\sqrt{{x}^{2}+2x+3}$的值域.分析 先求得函数的定义域为R,令x+1=t,可得函数y=t+$\sqrt{{t}^{2}+2}$-2,再利用二次函数的性质求得它的值域.
解答 解:由x2+2x+3≥0,求得x∈R,故函数的定义域为R.
令x+1=t,函数y=x-1+$\sqrt{{x}^{2}+2x+3}$=t+$\sqrt{{t}^{2}+2}$-2,
故当t=0时,函数y取得最小值为$\sqrt{2}$-2,显然,当t趋于正无穷大时,y的值趋于正无穷大.
故函数的值域为[$\sqrt{2}$-2,+∞).
点评 本题主要考查二次函数的性质的应用,体现了转化的数学思想,属于中档题.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
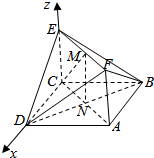 如图所示,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=$\sqrt{2}$,AF=1,M是线段EF的中点,N为AC与BD的交点,求点B到平面CMN的距离.
如图所示,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=$\sqrt{2}$,AF=1,M是线段EF的中点,N为AC与BD的交点,求点B到平面CMN的距离.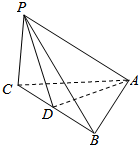 如图,△ABC是边长为2的等边三角形,PC⊥底面ABC,PC=2$\sqrt{2}$,求PA与侧面PBC所成角的大小.
如图,△ABC是边长为2的等边三角形,PC⊥底面ABC,PC=2$\sqrt{2}$,求PA与侧面PBC所成角的大小.