题目内容
当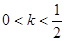 时,方程
时,方程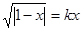 的解的个数是
的解的个数是
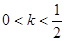 时,方程
时,方程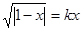 的解的个数是
的解的个数是| A.0 | B.1 | C.2 | D.3 |
D
分析:此题关键在于分类讨论,注意x>0的前提,讨论x的值,去绝对值,根据判别式进行判定根的个数.
解:方程两边平方|1-x|=(kx)2,并且由原方程还得出x>0
①x=1,左边=0,右边由于k≠0所以不为零.所以x=1不是解.
②x>1,去绝对值符号:x-1=k2x2即k2x2-x+1=0
判别式△=1-4k2由于0<k<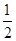 ,故△∈(0,1)所以有两个解.
,故△∈(0,1)所以有两个解.
当然还需要判断这两个解是不是都大于1的.的确,这是显然的,因为方程x-1=k2x2右边一定大于0,故两解一定是大于1的.
③x<1,去绝对值符号:1-x=k2x2即k2x2+x-1=0判别式△=1+4k2>0所以有两个解.
同样,因为方程1-x=k2x2右边一定大于0,故两解一定是小于1的.但是,还需要判断这两个解是否都大于零.
由根与系数的关系:两根之积:-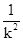 <0这就说明两根一正一负!那个负根是不能要的,所以舍去总共3个解
<0这就说明两根一正一负!那个负根是不能要的,所以舍去总共3个解
故选D.
解:方程两边平方|1-x|=(kx)2,并且由原方程还得出x>0
①x=1,左边=0,右边由于k≠0所以不为零.所以x=1不是解.
②x>1,去绝对值符号:x-1=k2x2即k2x2-x+1=0
判别式△=1-4k2由于0<k<
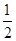 ,故△∈(0,1)所以有两个解.
,故△∈(0,1)所以有两个解.当然还需要判断这两个解是不是都大于1的.的确,这是显然的,因为方程x-1=k2x2右边一定大于0,故两解一定是大于1的.
③x<1,去绝对值符号:1-x=k2x2即k2x2+x-1=0判别式△=1+4k2>0所以有两个解.
同样,因为方程1-x=k2x2右边一定大于0,故两解一定是小于1的.但是,还需要判断这两个解是否都大于零.
由根与系数的关系:两根之积:-
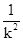 <0这就说明两根一正一负!那个负根是不能要的,所以舍去总共3个解
<0这就说明两根一正一负!那个负根是不能要的,所以舍去总共3个解故选D.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目

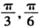 (单位:弧度/秒),M为线段PQ的中点,记经过x秒后(其中
(单位:弧度/秒),M为线段PQ的中点,记经过x秒后(其中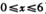 ),
),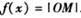
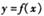 的函数解析式;
的函数解析式;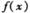 图象上的各点均向右平移2个单位长度,得到
图象上的各点均向右平移2个单位长度,得到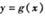 的图象,求函数
的图象,求函数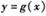 的单调递减区间.
的单调递减区间.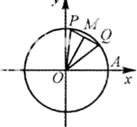
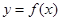 是函数
是函数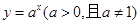 的反函数,其图像经过点
的反函数,其图像经过点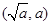 ,则
,则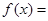 ( )
( )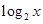
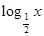
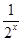
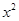
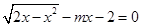 有两个不相等的实数解,则实数m的取值范围( )
有两个不相等的实数解,则实数m的取值范围( )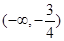
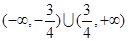
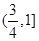
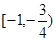
 .
.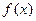 是定义在
是定义在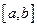 上的函数,其图像是一条连续的曲线,且满足下列条件:
上的函数,其图像是一条连续的曲线,且满足下列条件: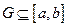 ;
;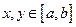 ,都有
,都有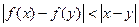 .
.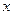 的方程
的方程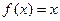 在区间
在区间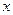 的方程
的方程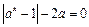 有两个相异的实根,则实数
有两个相异的实根,则实数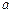 的取值范围是 ** .
的取值范围是 ** .