Question

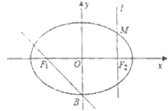
【题目】如图，圆与直线相切于点，与正半轴交于点，与直线在第一象限的交点为. 点为圆上任一点，且满足，以为坐标的动点的轨迹记为曲线．

（1）求圆的方程及曲线的方程；

（2）若两条直线和分别交曲线于点和，求四边形面积的最大值，并求此时的的值．

（3）已知曲线的轨迹为椭圆，研究曲线的对称性，并求椭圆的焦点坐标．

Answer 1

【答案】（1），（2）时，四边形的面积最大值为.（3）

【解析】

（1）由圆半径为圆心到切线距离得圆半径，从而得圆方程，由表示出点坐标代入圆方程可得曲线的方程．

（2）把方程代入曲线的方程求得的坐标，得，同理可得，由得，应用整体换元法结合基本不等式可求得最值（也可变形为，求最值）；

（3）由曲线的方程可得对称性：关于直线对称，关于原点对称，求出它与对称轴的交点即顶点坐标，得出，求出，从而可得焦点坐标．

解：（1）由题意圆的半径，

故圆的方程为.

由得，，将代入

得为曲线的方程.

（2）由

得,，

所以，同理.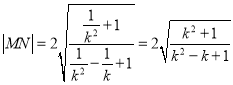

由题意知 ，所以四边形的面积.

∵ ，∴ .

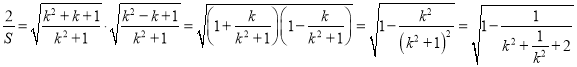
当且仅当时等号成立，此时.

∴ 当时，四边形的面积最大值为.

（3） 曲线的方程为，它关于直线、和原点对称，

下面证明：

设曲线上任一点的坐标为，则，点关于直线的对称点为，显然，所以点在曲线上，故曲线关于直线对称，

同理曲线关于直线和原点对称.

证明：求得和直线的交点坐标为，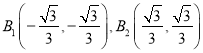

和直线的交点坐标为，

，，，.

在上取点 .

设为曲线上任一点，则

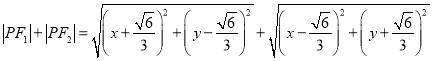
（因为）

.

即曲线上任一点到两定点的距离之和为定值.

若点到两定点的距离之和为定值，可以求得点的轨迹方程为（过程略）.

故曲线是椭圆，其焦点坐标为.