题目内容
【题目】如图,矩形ABCD和梯形BEFC所在平面互相垂直,∠BCF=∠CEF=90°,AD= ![]() .
.
(Ⅰ)求证:AE∥平面DCF;
(Ⅱ)当AB的长为何值时,二面角A﹣EF﹣C的大小为60°?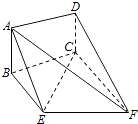
【答案】证明:(Ⅰ)过点E作EG⊥CF交CF于G,连接DG,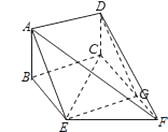
可得四边形BCGE为矩形.又ABCD为矩形,
所以AD⊥∥EG,从而四边形ADGE为平行四边形,故AE∥DG.
因为AE平面DCF,DG平面DCF,所以AE∥平面DCF.
(Ⅱ)解:过点B作BH⊥EF交FE的延长线于H,连接AH.
由平面ABCD⊥平面BEFG,AB⊥BC,得
AB⊥平面BEFC,
从而AH⊥EF,
所以∠AHB为二面角A﹣EF﹣C的平面角.
在Rt△EFG中,因为EG=AD= ![]() .
.
又因为CE⊥EF,所以CF=4,
从而BE=CG=3.
于是BH=BEsin∠BEH= ![]() .
.
因为AB=BHtan∠AHB,
所以当AB= ![]() 时,二面角A﹣EF﹣G的大小为60°
时,二面角A﹣EF﹣G的大小为60°
【解析】(Ⅰ)过点E作EG⊥CF并CF于G,连接DG,证明AE平行平面DCF内的直线DG,即可证明AE∥平面DCF;
(Ⅱ)过点B作BH⊥EF交FE的延长线于H,连接AH,说明∠AHB为二面角A﹣EF﹣C的平面角,通过二面角A﹣EF﹣C的大小为60°,求出AB即可.
【考点精析】根据题目的已知条件,利用直线与平面平行的判定的相关知识可以得到问题的答案,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.

 名校课堂系列答案
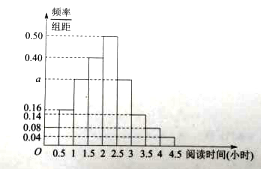
名校课堂系列答案【题目】某市环保局空气质量监控过程中,每隔x天作为一个统计周期.最近x天统计数据如表
空气污染指数 | [0,50] | (50,100] | (100,150] | (150,200] |
天数 | 15 | 40 | 35 | y |
(Ⅰ)根据所给统计表和频率分布直方图中的信息求出x,y的值,并完成频率分布直方图;
(Ⅱ)为了创生态城市,该市提出要保证每个统计周期“空气污染指数大于150μg/m3的天数占比不超过15%,平均空气污染指数小于100μg/m3”,请问该统计周期有没有达到预期目标.