��Ŀ����
����Ŀ��ijУΪ�˽��һѧ����ĩ�ġ��Ķ�ʱ�䡱���Ӹ�һ�꼶�������ȡ��![]() ��ѧ�����е��ˣ������ÿ�˵���ĩ���Ķ�ʱ�䡱����λ��Сʱ��������
��ѧ�����е��ˣ������ÿ�˵���ĩ���Ķ�ʱ�䡱����λ��Сʱ��������![]() �ֳ�
�ֳ�![]() �飬�Ƴ�������Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ��
�飬�Ƴ�������Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ��
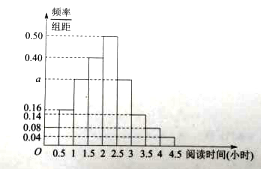
������ͼ��![]() ��ֵ��
��ֵ��
�����Ƹ�У��һѧ����ĩ���Ķ�ʱ�䡱����λ����
����������Ƶ�ʴ������. �ִ�ȫУ��һ�꼶�����ȡ![]() ��ѧ����������
��ѧ����������![]() ��ѧ�����Ķ�ʱ�䡱��
��ѧ�����Ķ�ʱ�䡱��![]() Сʱ�ڵĸ���Ϊ
Сʱ�ڵĸ���Ϊ![]() ������
������![]() .��
.��![]() ȡ���ʱ����
ȡ���ʱ����![]() ��ֵ.
��ֵ.
���𰸡�����![]() ; ����
; ����![]() ;����
;����![]() .
.
�����������������
��������Ƶ�ʷֲ�ֱ��ͼ������С���������Ƶ�ʣ�֮��Ϊ1�����![]() ��
��
������λ�����ǰ�ֱ��ͼ����С�������ƽ�ֵ���һ�㣻
������ȡ����![]() ��ѧ���У���ĩ�Ķ�ʱ����
��ѧ���У���ĩ�Ķ�ʱ����![]() �е���
�е���![]() �ˣ���
�ˣ���![]() ���Ӷ���ֲ�
���Ӷ���ֲ�![]() ���ɴ˿ɵ�
���ɴ˿ɵ�![]() ������
������![]() .�������
.�������![]() �����
�����![]() �����ֵ��
�����ֵ��
���������
����
��Ƶ�ʷֲ�ֱ��ͼ����֪��
��ĩ�ġ��Ķ�ʱ�䡱��![]() ��Ƶ��Ϊ
��Ƶ��Ϊ![]() .
.
ͬ������![]() �����Ƶ�ʷֱ�Ϊ
�����Ƶ�ʷֱ�Ϊ![]() ��
��
�� ![]()
���![]() .
.
��������λ��Ϊ![]() Сʱ.
Сʱ.
��Ϊǰ![]() ���Ƶ��֮��Ϊ
���Ƶ��֮��Ϊ ![]() ��
��
��ǰ![]() ���Ƶ��֮��Ϊ
���Ƶ��֮��Ϊ ![]() ��
��
����![]() .
.
�� ![]() �����
�����![]() .
.
�ʿɹ��Ƹ�У��һѧ����ĩ���Ķ�ʱ�䡱����λ��Ϊ![]() Сʱ.
Сʱ.
��������ȡ����![]() ��ѧ���У���ĩ�Ķ�ʱ����
��ѧ���У���ĩ�Ķ�ʱ����![]() �е���
�е���![]() �ˣ���
�ˣ���![]() ���Ӷ���ֲ�����
���Ӷ���ֲ�����![]() ����ǡ����
����ǡ����![]() ��ѧ����ĩ�Ķ�ʱ����
��ѧ����ĩ�Ķ�ʱ����![]() �еĸ���Ϊ
�еĸ���Ϊ
![]() ������
������![]() .
.
��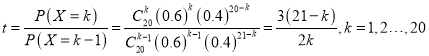 .
.
��![]() ����
����![]() ��
��
��![]() ����
����![]() .
.
���Ե�![]() ʱ��
ʱ�� ![]() ���.
���.
����![]() ��ȡֵΪ
��ȡֵΪ![]() .
.

 ���100��1�ž�ϵ�д�
���100��1�ž�ϵ�д�