题目内容
【题目】某高新技术公司要生产一批新研发的![]() 款手机和
款手机和![]() 款手机,生产一台
款手机,生产一台![]() 款手机需要甲材料
款手机需要甲材料![]() ,乙材料
,乙材料![]() ,并且需要花费1天时间,生产一台
,并且需要花费1天时间,生产一台![]() 款手机需要甲材料
款手机需要甲材料![]() ,乙材料
,乙材料![]() ,也需要1天时间,已知生产一台
,也需要1天时间,已知生产一台![]() 款手机利润是1000元,生产一台
款手机利润是1000元,生产一台![]() 款手机的利润是2000元,公司目前有甲、乙材料各,则在
款手机的利润是2000元,公司目前有甲、乙材料各,则在![]() 不超过120天的情况下,公司生产两款手机的最大利润是__________元.
不超过120天的情况下,公司生产两款手机的最大利润是__________元.
【答案】210000
【解析】设生产![]() 款手机和
款手机和![]() 款手机
款手机![]() 、
、![]() 件,利润之和为
件,利润之和为![]() 元,则根据题意可得
元,则根据题意可得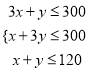 ,目标函数为
,目标函数为![]()
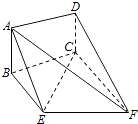
,目标函数![]() 表示直线
表示直线![]() 的纵轴截距的2000倍,由图可知,当直线
的纵轴截距的2000倍,由图可知,当直线![]() 经过点
经过点![]() 点时,
点时, ![]() 取得最大值。联立方程
取得最大值。联立方程![]() ,解得
,解得![]() .所以当
.所以当![]() ,时,目标函数取得最大值,
,时,目标函数取得最大值, ![]() .
.
点晴:本题考查的是线性规划问题,线性规划问题的实质是把代数问题几何化,即数形结合的思想,需要注意的是:一,准确无误地作出可行域;二,画目标函数所对应的直线时,要注意与约束条件中的直线的斜率进行比较,避免出错;三,一般情况下,目标函数的最值会在可行域的端点或边界上取得.

练习册系列答案
相关题目
【题目】某公司生产![]() 、
、![]() 两种产品,且产品的质量用质量指标来衡量,质量指标越大表明产品质量越好.现按质量指标划分:质量指标大于或等于82为一等品,质量指标小于82为二等品.现随机抽取这两种产品各100件进行检测,检测结果统计如表:
两种产品,且产品的质量用质量指标来衡量,质量指标越大表明产品质量越好.现按质量指标划分:质量指标大于或等于82为一等品,质量指标小于82为二等品.现随机抽取这两种产品各100件进行检测,检测结果统计如表:
测试指标 |
|
|
|
|
|
产品 | 8 | 12 | 40 | 32 | 8 |
产品 | 7 | 18 | 40 | 29 | 6 |
(Ⅰ)请估计![]() 产品的一等奖;
产品的一等奖;
(Ⅱ)已知每件![]() 产品的利润
产品的利润![]() (单位:元)与质量指标值
(单位:元)与质量指标值![]() 的关系式为:
的关系式为: 
已知每件![]() 产品的利润
产品的利润![]() (单位:元)与质量指标值
(单位:元)与质量指标值![]() 的关系式为:
的关系式为: 
(i)分别估计生产一件![]() 产品,一件
产品,一件![]() 产品的利润大于0的概率;
产品的利润大于0的概率;
(ii)请问生产![]() 产品,
产品, ![]() 产品各100件,哪一种产品的平均利润比较高.
产品各100件,哪一种产品的平均利润比较高.