Question

【题目】已知椭圆过点，且右焦点为．

（1）求椭圆的方程；

（2）过点的直线与椭圆交于两点，交轴于点．若，求证：为定值；

（3）在（2）的条件下，若点不在椭圆的内部，点是点关于原点的对称点，试求三角形面积的最小值．

Answer 1

【答案】（1）（2）见解析（3）

【解析】

（1）由题意b=2，c=2，所以，椭圆C的方程为。

(2)设A、B、P的坐标分别为。

由知，。

又点A在椭圆C上，则

，

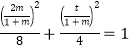整理得。

由，同理得到

。

由于A、B不重合，即，故m、n是二次方程

的两根，所以m+n=-4，为定值。

（3）依题意，直线l的方程为，即，与椭圆C的方程联立，消去y并整理，得

，

，

所以，而

。

由已知，点P不在椭圆C的内部，得，即，所以的最小值为，故三角形QAB面积的最小值为。