题目内容
【题目】冬季历来是交通事故多发期,面临着货运高危运行、恶劣天气频发、包车客运监管漏洞和农村交通繁忙等四个方面的挑战.全国公安交管部门要认清形势、正视问题,针对近期事故暴露出来的问题,强薄羽、补短板、堵漏洞,进一步推动五大行动,巩固扩大五大行动成果,全力确保冬季交通安全形势稳定.据此,某网站推出了关于交通道路安全情况的调查,通过调查年龄在![]() 的人群,数据表明,交通道路安全仍是百姓最为关心的热点,参与调查者中关注此类问题的约占80%,现从参与调查并关注交通道路安全的人群中随机选出100人,并将这100人按年龄分组:第1组
的人群,数据表明,交通道路安全仍是百姓最为关心的热点,参与调查者中关注此类问题的约占80%,现从参与调查并关注交通道路安全的人群中随机选出100人,并将这100人按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
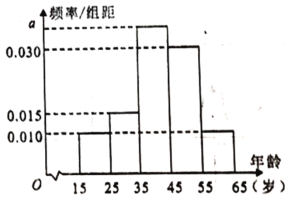
(1)求这100人年龄的样本平均数(同一组数据用该区间的中点值作代表)和中位数(精确到小数点后一位);
(2)现在要从年龄较大的第4,5组中用分层抽样的方法抽取8人,再从这8人中随机抽取3人进行问卷调查,求第4组恰好抽到2人的概率;
(3)若从所有参与调查的人(人数很多)中任意选出3人,设其中关注交通道路安全的人数为随机变量X,求X的分布列与数学期望.
【答案】(1)平均数为![]() 岁;中位数为
岁;中位数为![]() 岁(2)
岁(2)![]() (3)详见解析
(3)详见解析
【解析】
(1)由频率分布直方图能求出![]() ,由此能求出这
,由此能求出这![]() 人年龄的样本平均数和中位数;
人年龄的样本平均数和中位数;
(2)第4,5组抽取的人数分别为6人,2人,设第4组中恰好抽取2人的事件为![]() ,利用排列组合能求出事件
,利用排列组合能求出事件![]() 的概率;
的概率;
(3)从所有参与调查的人中任意选出1人,关注交通道路安全的概率为![]() ,
,![]() 的所有可能取值为0,1,2,3,
的所有可能取值为0,1,2,3,![]() ,分别求出相应的概率,由此能求出
,分别求出相应的概率,由此能求出![]() 的分布列和数学期望.
的分布列和数学期望.
解:(1)由![]() ,得
,得![]() ,
,
平均数为![]() 岁;
岁;
设中位数为x,则![]() ,∴
,∴![]() 岁.
岁.
(2)第4,5组抽取的人数分别为6人,2人.
设第4组中恰好抽取2人的事件为A,则![]() .
.
(3)从所有参与调查的人中任意选出1人,关注交通道路安全的概率为![]() ,
,
X的所有可能取值为0,1,2,3,
∴![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
所以X的分布列为:
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
∵![]() ,∴
,∴![]() .
.

 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案【题目】某校高三实验班的60名学生期中考试的语文、数学成绩都在![]() 内,其中语文成绩分组区间是:
内,其中语文成绩分组区间是:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .其成绩的频率分布直方图如图所示,这60名学生语文成绩某些分数段的人数
.其成绩的频率分布直方图如图所示,这60名学生语文成绩某些分数段的人数![]() 与数学成绩相应分数段的人数
与数学成绩相应分数段的人数![]() 之比如下表所示:
之比如下表所示:
分组区间 |
|
|
|
|
|
|
|
|
|
| |
语文人数 | 24 | 3 | |||
数学人数 | 12 | 4 |
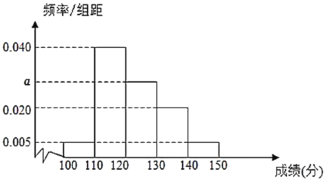
(1)求图中![]() 的值及数学成绩在
的值及数学成绩在![]() 的人数;
的人数;
(2)语文成绩在![]() 的3名学生均是女生,数学成绩在
的3名学生均是女生,数学成绩在![]() 的4名学生均是男生,现从这7名学生中随机选取4名学生,事件
的4名学生均是男生,现从这7名学生中随机选取4名学生,事件![]() 为:“其中男生人数不少于女生人数”,求事件
为:“其中男生人数不少于女生人数”,求事件![]() 发生的概率;
发生的概率;
(3)若从数学成绩在![]() 的学生中随机选取2名学生,且这2名学生中数学成绩在
的学生中随机选取2名学生,且这2名学生中数学成绩在![]() 的人数为
的人数为![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.