题目内容
【题目】已知函数![]() .
.
(Ⅰ)求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)若函数![]() 在区间
在区间![]() 上存在极值,求实数
上存在极值,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)设![]() ,对任意
,对任意![]() 恒有
恒有![]() ,求实数
,求实数![]() 的取值范围。
的取值范围。
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)
;(Ⅲ)![]() .
.
【解析】
(Ⅰ)求出导函数得到斜率,利用点斜式得到切线方程;
(Ⅱ)求出函数的极值,再探讨函数在区间 (m,m![]() )(其中a>0)上存在极值,寻找关于m的不等式,求出实数m的取值范围;
)(其中a>0)上存在极值,寻找关于m的不等式,求出实数m的取值范围;
(Ⅲ)先求导,再构造函数h(x)=lnx![]() ,求出h(x)的最大值小于0即可.
,求出h(x)的最大值小于0即可.
解:(I). ![]()
故切线的斜率为![]() ,又f(e)=
,又f(e)=![]()
∴切线方程为:![]() ,即
,即![]()
(II).当![]() 时,
时,![]()
当x>l时,![]()
f(x)在(0,1)上单调递增,在(1.+![]() )上单调递减。
)上单调递减。
故f(x)在x=l处取得极大值。
∵f(x)在区间(m,m+![]() )(m>0)上存在极值,
)(m>0)上存在极值,
∴0<m<1且m+![]() >1,解得
>1,解得![]()
(Ⅲ).由题可知.a≠0,且![]()
![]() ,
,
![]() ,
,
当a<0时,g(x)>0.不合题意。
当a>0时,由![]() 可得
可得![]() 恒成立
恒成立
设![]() ,则
,则![]()
求导得: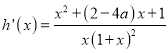
设![]()
①当0<a≤l时,△≤0,此时:![]()
∴h(x)在(0,1)内单调递增,又h(l)=0,所以h(x)<h(l)=0.
所以0<a≤l符合条件.
②当a>1时,△>0,注意到t(0)=1,t(1)=4(1-a)<0,存在xo![]() (0,1),使得t(x0)=0,
(0,1),使得t(x0)=0,
于是对任意![]() ,t(x)<0,h’(x)<0.则h(x)在(xo,1)内单调递减,又h(l)=0,所以当
,t(x)<0,h’(x)<0.则h(x)在(xo,1)内单调递减,又h(l)=0,所以当![]() 时,h(x)>0,不合要求,
时,h(x)>0,不合要求,
综合①②可得0<a≤1

练习册系列答案
相关题目