题目内容
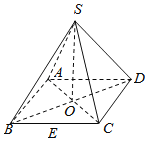
【题目】如图,四棱锥![]() 中,底面是边长为
中,底面是边长为![]() 的正方形ABCD,AC与BD的交点为O,
的正方形ABCD,AC与BD的交点为O,![]() 平面ABCD且
平面ABCD且![]() ,E是边BC的中点,动点P在四棱锥表面上运动,并且总保持
,E是边BC的中点,动点P在四棱锥表面上运动,并且总保持![]() ,则动点P的轨迹的周长为( )
,则动点P的轨迹的周长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
分别取CD、SC的中点F、G,连接EF、FG和EG,证明平面EFG∥平面BDS,再由题意证明AC⊥平面EFG,得出点P在△EFG的三条边上,求出△EFG的周长即可.
解:分别取CD、SC的中点F、G,连接EF、FG和EG,如图所示;
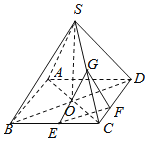
则EF∥BD,EF平面BDS,BD 平面BDS
∴EF∥平面BDS
同理FG∥平面BDS
又EF∩FG=F,EF 平面EFG,FG 平面EFG,,
∴平面EFG∥平面BDS,
由AC⊥BD,AC⊥SO,且AC∩SO=O,
则AC⊥平面BDS,
∴AC⊥平面EFG,
∴点P在△EFG的三条边上;
又EF=![]() BD=
BD=![]() ×
×![]() ×
×![]() =1,
=1,
FG=EG=![]() SB=
SB=![]() ×
×![]() =
=![]() ,
,
∴△EFG的周长为EF+2FG=1+![]() .
.
故选:D.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目




