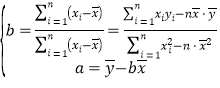题目内容
【题目】判断下列命题的真假:
(1)![]() 是有理数;(2)
是有理数;(2)![]() ;
;
(3)奇数的平方仍是奇数;(4)两个集合的交集还是一个集合;
(5)每一个素数都是奇数;(6)方程![]() 有实数根;
有实数根;
(7)![]() ;(8)如果
;(8)如果![]() ,那么
,那么![]() .
.
【答案】(1)假;(2)假;(3)真;(4)真;(5)假;(6)假;(7)真;(8)假
【解析】
(1)根据有理数的定义判定即可.
(2)直接计算分析即可.
(3)根据奇数的性质判断即可.
(4)根据集合的运算判断即可.
(5)举出反例即可.
(6)求解分析判定即可.
(7)直接计算即可.
(8)举出反例即可.
(1)![]() 中
中![]() 为无理数.故
为无理数.故![]() 是无理数,故 (1)为假命题.
是无理数,故 (1)为假命题.
(2) ![]() ,故(2)为假命题.
,故(2)为假命题.
(3)因为奇数的平方为奇数,故(3)为真命题.
(4)集合求交集后仍然是集合,故(4)为真命题.
(5)2是素数但2是偶数.故(5)为假命题.
(6) ![]() 即
即![]() 无实数解.故(6)为假命题.
无实数解.故(6)为假命题.
(7) ![]() .故(7)为真命题.
.故(7)为真命题.
(8)如![]() ,满足
,满足![]() 但不满足
但不满足![]() .故(8)为假命题.
.故(8)为假命题.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
【题目】某名校从![]() 年到
年到![]() 年考入清华,北大的人数可以通过以下表格反映出来。(为了方便计算,将
年考入清华,北大的人数可以通过以下表格反映出来。(为了方便计算,将![]() 年编号为
年编号为![]() ,
,![]() 年编为
年编为![]() ,以此类推……)
,以此类推……)
年份 |
|
|
|
|
|
|
|
|
|
|
人数 |
|
|
|
|
|
|
|
|
|
|
(1)将这![]() 年的数据分为人数不少于
年的数据分为人数不少于![]() 人和少于
人和少于![]() 人两组,按分层抽样抽取
人两组,按分层抽样抽取![]() 年,问考入清华、北大的人数不少于20的应抽多少年?在抽取的这
年,问考入清华、北大的人数不少于20的应抽多少年?在抽取的这![]() 年里,若随机的抽取两年恰有一年考入清华、北大的人数不少于
年里,若随机的抽取两年恰有一年考入清华、北大的人数不少于![]() 的概率是多少?;
的概率是多少?;
(2)根据最近![]() 年的数据,利用最小二乘法求出与之间的线性回归方程,并用以预测
年的数据,利用最小二乘法求出与之间的线性回归方程,并用以预测![]() 年该校考入清华、北大的人数。(结果要求四舍五入至个位)
年该校考入清华、北大的人数。(结果要求四舍五入至个位)
参考公式: