题目内容
17. 在扇形AOB中,OA⊥OB,以OA,OB为直径的半圆交于点C,点P在如图所示图形的阴影区域中(含边界),若→OP−−→OP=x→OA−−→OA+y→OB−−→OB(x,y∈R),则2x+y的取值范围是( )
在扇形AOB中,OA⊥OB,以OA,OB为直径的半圆交于点C,点P在如图所示图形的阴影区域中(含边界),若→OP−−→OP=x→OA−−→OA+y→OB−−→OB(x,y∈R),则2x+y的取值范围是( )| A. | [0,√22√22] | B. | [√22√22,√2√2] | C. | [1,√5√5] | D. | [√5√5,2√2√2] |
分析 以OA所在直线为x轴,以OB所在直线为y轴建立平面直角坐标系,由向量相等得到P的坐标,写出P的坐标所满足的关系式,由线性规划知识求得答案.
解答 解: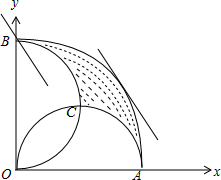 以OA所在直线为x轴,以OB所在直线为y轴建立平面直角坐标系,
以OA所在直线为x轴,以OB所在直线为y轴建立平面直角坐标系,
则可设A(1,0),B(0,1),
∴→OP−−→OP=x→OA−−→OA+y→OB−−→OB=(x,0)+(0,y)=(x,y),
则x,y满足条件{0≤x≤10≤y≤1(x−12)2+y2≥14x2+(y−12)2≥14x2+y2≤1,
作出可行域如图,
令z=2x+y,由|−z|√22+12=1,的z=±√5,
∵x≥0,y≥0,∴z=√5;
化目标函数z=2x+y为y=-2x+z,
由图可知,当直线y=-2x+z过点B(0,1)时,直线在y轴上的截距最小,z有最小值1.
故选:C.
点评 本题考查了简单的线性规划,考查了数形结合的解题思想方法和数学转化思想方法,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.函数f(x)=e-x+a,g(x)=|lnx|,若x1,x2都满足f(x)=g(x),则( )
| A. | x1•x2>e | B. | 1<x1•x2<e | C. | 0<x1•x2<e-1 | D. | e-1<x1•x2<1 |