题目内容
8．函数f（x）=e-x+a，g（x）=|lnx|，若x1，x2都满足f（x）=g（x），则（ ）| A． | x1•x2＞e | B． | 1＜x1•x2＜e | C． | 0＜x1•x2＜e-1 | D． | e-1＜x1•x2＜1 |
分析 画出图象得出f（x1）=g（x1），f（x2）=g（x2），x1＞1，0＜x2＜1，利用图象得出范围-1＜e${\;}^{-{x}_{1}}$$-{e}^{-{x}_{2}}$=lnx1x2＜0，求解即可得出e-1＜x1x2＜1．
解答 解：∵函数f（x）=e-x+a，g（x）=|lnx|，
∵f（x1）=g（x1），f（x2）=g（x2），x1＞1，0＜x2＜1
∴e${\;}^{-{x}_{1}}$+a=lnx1，e${\;}^{-{x}_{2}}$+a=-lnx2，
即-1＜e${\;}^{-{x}_{1}}$$-{e}^{-{x}_{2}}$=lnx1x2＜0，
e-1＜x1x2＜1，
故选：D．
点评 本题考查了函数的性质，函数的零点的求解，学生运用函数图象解决问题的能力，观察变化的能力，属于中档题．
练习册系列答案
相关题目
19．已知抛物线C：x2=16y的焦点为F，准线为l，M是l上一点，P是直线MF与C的一个交点，若$\overrightarrow{FM}$=3$\overrightarrow{FP}$，则|PF|=（ ）
| A． | $\frac{16}{3}$ | B． | $\frac{8}{3}$ | C． | $\frac{5}{3}$ | D． | $\frac{5}{2}$ |
16．已知函数f（x）=lg$\frac{1+x}{1-x}$，则“x＜$\frac{9}{11}$”是“f（x）＜1成立的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
17．
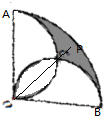在扇形AOB中，OA⊥OB，以OA，OB为直径的半圆交于点C，点P在如图所示图形的阴影区域中（含边界），若$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$（x，y∈R），则2x+y的取值范围是（ ）
在扇形AOB中，OA⊥OB，以OA，OB为直径的半圆交于点C，点P在如图所示图形的阴影区域中（含边界），若$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$（x，y∈R），则2x+y的取值范围是（ ）| A． | [0，$\frac{\sqrt{2}}{2}$] | B． | [$\frac{\sqrt{2}}{2}$，$\sqrt{2}$] | C． | [1，$\sqrt{5}$] | D． | [$\sqrt{5}$，2$\sqrt{2}$] |