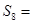题目内容
(10分) 已知数列{an}的前n项和Sn=10n-n2,(n∈N*).
(1)求a1和an;
(2)记bn=|an|,求数列{bn}的前n项和.
(1)求a1和an;
(2)记bn=|an|,求数列{bn}的前n项和.
(1) an=-2n+11(n∈N*).(2) Tn=

本题考查数列前n项和与通项公式的应用,考查转化思想与计算能力
由Sn=10n-n2知Sn是关于n的无常数项的二次函数(n∈N*),可知{an}为等差数列,求出an,然后再判断哪些项为正,哪些项为负,然后求解Tn.
(1)∵Sn=10n-n2,∴a1=S1=10-1=9.
∵Sn=10n-n2,当n≥2,n∈N*时,
Sn-1=10(n-1)-(n-1)2=10n-n2+2n-11,
∴an=Sn-Sn-1=(10n-n2)-(10n-n2+2n-11)
=-2n+11.
又n=1时,a1=9=-2×1+11,符合上式.
则数列{an}的通项公式为an=-2n+11(n∈N*).
(2)∵an=-2n+11,∴bn=|an|=
设数列{bn}的前n项和为Tn,
n≤5时,Tn= =10n-n2;
=10n-n2;
n>5时Tn=T5+ =25+
=25+ =25+(n-5)2=n2-10n+50,
=25+(n-5)2=n2-10n+50,
∴数列{bn}的前n项和Tn=
由Sn=10n-n2知Sn是关于n的无常数项的二次函数(n∈N*),可知{an}为等差数列,求出an,然后再判断哪些项为正,哪些项为负,然后求解Tn.
(1)∵Sn=10n-n2,∴a1=S1=10-1=9.
∵Sn=10n-n2,当n≥2,n∈N*时,
Sn-1=10(n-1)-(n-1)2=10n-n2+2n-11,
∴an=Sn-Sn-1=(10n-n2)-(10n-n2+2n-11)
=-2n+11.
又n=1时,a1=9=-2×1+11,符合上式.
则数列{an}的通项公式为an=-2n+11(n∈N*).
(2)∵an=-2n+11,∴bn=|an|=

设数列{bn}的前n项和为Tn,
n≤5时,Tn=
 =10n-n2;
=10n-n2; n>5时Tn=T5+
 =25+
=25+ =25+(n-5)2=n2-10n+50,
=25+(n-5)2=n2-10n+50,∴数列{bn}的前n项和Tn=


练习册系列答案
相关题目
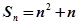 ,那么它的通项公式为an=_________
,那么它的通项公式为an=_________ 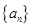 中,
中,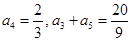 .
. ,且
,且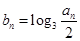 ,求数列
,求数列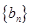 的前
的前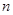 项和
项和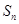 .
.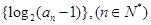 为等差数列,且
为等差数列,且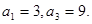 求
求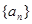 的通项式;
的通项式;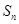 。
。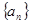 的前
的前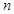 项和为
项和为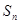 ,且
,且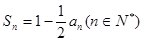
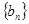 的通项公式
的通项公式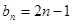 ,记
,记 ,求数列
,求数列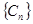 的前
的前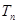 .
.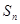 ﹥0成立的最大自然数n的值为.
﹥0成立的最大自然数n的值为. 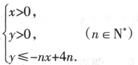 表示的平面区域为
表示的平面区域为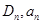 表示区域Dn中整点的个数(其中整点是指横、纵坐标都是整数的点),则
表示区域Dn中整点的个数(其中整点是指横、纵坐标都是整数的点),则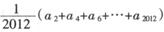 =( )
=( )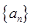 的通项公式是
的通项公式是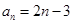 ,将数列中各项进行如下分组:第1组1个数(
,将数列中各项进行如下分组:第1组1个数(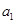 ),第2 组2个数(
),第2 组2个数(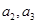 )第3组3个数(
)第3组3个数(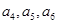 ),依次类推,……,则第16组的第10个数是 __________________.
),依次类推,……,则第16组的第10个数是 __________________.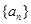 中,
中,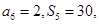 则
则