题目内容
在等比数列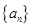 中,
中,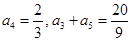 .
.
(Ⅰ)求数列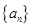 的通项公式;
的通项公式;
(Ⅱ)若数列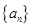 的公比大于
的公比大于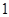 ,且
,且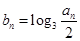 ,求数列
,求数列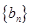 的前
的前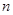 项和
项和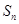 .
.
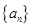 中,
中,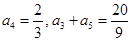 .
.(Ⅰ)求数列
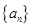 的通项公式;
的通项公式;(Ⅱ)若数列
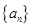 的公比大于
的公比大于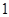 ,且
,且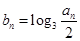 ,求数列
,求数列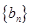 的前
的前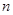 项和
项和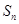 .
.(Ⅰ)2×3n-5(Ⅱ)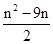
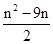
(1)先根据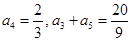 建立关于
建立关于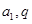 的两个方程,解出
的两个方程,解出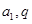 的值,进而得到
的值,进而得到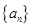 的通项公式.
的通项公式.
(II)在(I)的基础上可得到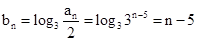 ,从而可知
,从而可知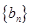 是等差数列,从而可求出其首项和公差,进而根据前n项和公式求出Sn.
是等差数列,从而可求出其首项和公差,进而根据前n项和公式求出Sn.
解:(Ⅰ)设等比数列{an}的公比为q, 则q≠0, a3=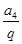 =
= 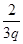 , a5=a4q=
, a5=a4q=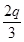
所以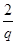 + 2q=
+ 2q=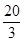 , 解得q1=
, 解得q1= 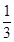 , q2= 3, …………4分
, q2= 3, …………4分
当q1=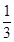 , a1=18.所以 an=18×(
, a1=18.所以 an=18×( 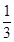 )n-1=
)n-1=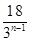 = 2×33-n.
= 2×33-n.
当q=3时, a1=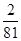 ,所以an=
,所以an=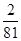 ×
×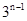 =2×3n-5. …………6分
=2×3n-5. …………6分
(Ⅱ)由(Ⅰ)及数列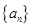 公比大于
公比大于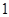 ,得q=3,an=2×3n-5 ,…………8分
,得q=3,an=2×3n-5 ,…………8分
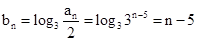 ,
,
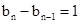 (常数),
(常数), 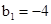 .
.
所以数列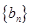 为首项为-4,公差为1的等差数列,……10分
为首项为-4,公差为1的等差数列,……10分
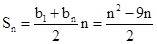 . …………12分
. …………12分
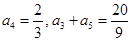 建立关于
建立关于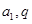 的两个方程,解出
的两个方程,解出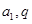 的值,进而得到
的值,进而得到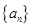 的通项公式.
的通项公式.(II)在(I)的基础上可得到
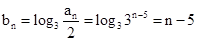 ,从而可知
,从而可知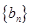 是等差数列,从而可求出其首项和公差,进而根据前n项和公式求出Sn.
是等差数列,从而可求出其首项和公差,进而根据前n项和公式求出Sn.解:(Ⅰ)设等比数列{an}的公比为q, 则q≠0, a3=
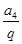 =
= 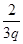 , a5=a4q=
, a5=a4q=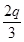
所以
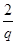 + 2q=
+ 2q=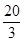 , 解得q1=
, 解得q1= 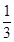 , q2= 3, …………4分
, q2= 3, …………4分当q1=
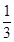 , a1=18.所以 an=18×(
, a1=18.所以 an=18×( 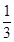 )n-1=
)n-1=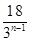 = 2×33-n.
= 2×33-n. 当q=3时, a1=
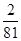 ,所以an=
,所以an=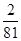 ×
×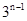 =2×3n-5. …………6分
=2×3n-5. …………6分(Ⅱ)由(Ⅰ)及数列
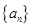 公比大于
公比大于 ,得q=3,an=2×3n-5 ,…………8分
,得q=3,an=2×3n-5 ,…………8分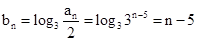 ,
,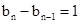 (常数),
(常数), 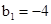 .
.所以数列
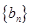 为首项为-4,公差为1的等差数列,……10分
为首项为-4,公差为1的等差数列,……10分 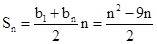 . …………12分
. …………12分
练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
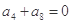 ,则使前n项和Sn取最值的正整数n="__________" .
,则使前n项和Sn取最值的正整数n="__________" .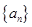 中,
中,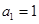 ,前
,前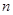 项和
项和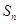 满足条件
满足条件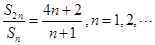 .
.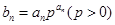 ,求数列
,求数列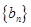 的前
的前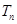 .
.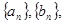 前
前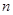 项和分别为
项和分别为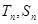 ,
,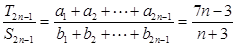 ,则
,则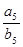 =_____.
=_____.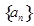 的前
的前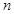 项和为
项和为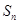 ,且
,且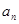 是
是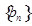 中,
中,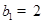 ,点
,点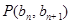 在直线
在直线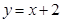 上.
上.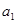 和
和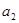 的值;
的值;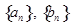 的通项
的通项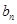 ;
;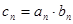 ,求数列
,求数列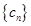 的前n项和
的前n项和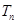 .
. 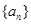 为等差数列,且
为等差数列,且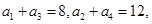
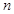 项和为
项和为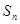 ,若
,若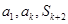 成等比数列,求正整数
成等比数列,求正整数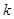 的值。
的值。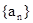 的公差为2,若
的公差为2,若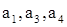 成等比数列,则
成等比数列,则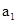 =
=