��Ŀ����
����Ŀ��Ϊ�˶�2016��ijУ�п��ɼ����з�������60�����ϵ�ȫ��ͬѧ��������8λ�����ǵ���ѧ������������Ϊ�ٷ��ƣ���С��������60��65��70��75��80��85��90��95������������С��������72��77��80��84��88��90��93��95�� �ο���ʽ�����ϵ�� 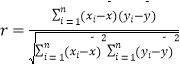 ��
��
�ع�ֱ�߷����ǣ� ![]() ������
������  ��
��
�ο����ݣ� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
��
��1�����涨85������Ϊ���㣬����8λͬѧ��ǡ��3λͬѧ����ѧ������������Ϊ����ĸ��ʣ�
��2������8λͬѧ����ѧ����������ѧ������ʵ�϶�Ӧ���±���
ѧ����� | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
��ѧ����x | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 |
��������y | 72 | 77 | 80 | 84 | 88 | 90 | 93 | 95 |
��ѧ����z | 67 | 72 | 76 | 80 | 84 | 87 | 90 | 92 |
���ñ���y��x��z��x�����ϵ��˵����������ѧ����ѧ����ѧ����س̶ȣ�
����y��x��z��x�����Իع鷽�̣�ϵ����ȷ��0.01������ijͬѧ����ѧ�ɼ�Ϊ50��ʱ����������������ѧ���Ƶĵ÷֣�
���𰸡�
��1���⣺��8λͬѧ��ǡ��3λͬѧ����ѧ������������Ϊ���㣬
����Ҫ�ȴ�����4 �����������ѡ��3������ѧ������Ӧ��
��ͬ�������� ![]() ����
���� ![]() ����
����
Ȼ��ʣ�µ�5����ѧ�������������������Ӧ����ͬ�������� ![]() ��
��
���ݳ˷�ԭ�������������IJ�ͬ������ ![]() ��
��
��8λͬѧ��������������ѧ�����ֱ��Ӧ�������� ![]() ��
��
������ĸ���Ϊ ![]()
��2���⣺�ٱ���y��x��z��x�����ϵ���ֱ���
![]() ��
��
���Կ�������������ѧ����ѧ����ѧ�ɼ����Ǹ߶�����أ�
����y��x��z��x�����Իع鷽�̷ֱ��� ![]() ��
��
�������������ݣ������
![]() ��
��
![]() ��
��
����y��x��z��x�Ļع鷽�̷ֱ���
![]() ��
�� ![]() ��
��
��x=50ʱ�� ![]() ��
��
�൱��������ѧΪ50��ʱ������������ѧ�ɼ��ֱ�ԼΪ66.85�֡�61.2��
����������1���������8λͬѧ��ǡ��3λͬѧ����ѧ������������Ϊ����Ļ����¼������Լ���8λͬѧ��������������ѧ�����ֱ��Ӧ�����¼�������������ĸ���ֵ��2���ٱ���y��x��z��x�����ϵ�����ó���������ѧ����ѧ����ѧ�ɼ����Ǹ߶�����أ������y��x��z��x�����Իع鷽�̣��ɴ˼���x=50ʱy��z��ֵ���ɣ�

 ȫ�ŵ�����Ԫ�ƻ�ϵ�д�
ȫ�ŵ�����Ԫ�ƻ�ϵ�д�����Ŀ��ijƶ��������1500������,����ƽԭ����1050��,ɽ��450��,Ϊ����õ���2017���ͥ�������,�Ӷ����õ�ʵʩ������ƶ��,���÷ֲ�����ķ���,�ռ���150����ͥ2017�����������������(��λ:��Ԫ)
(I)Ӧ�ռ����ٻ�ɽ����ͥ����������?
(��)������150����������,�õ�2017���ͥ�����Ƶ�ʷֲ�ֱ��ͼ(��ͼ��ʾ),�����������ݷ�������Ϊ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .�����Ƶ������Ϊ����,���Ƹõ���2017���ͥ���볬��1.5��Ԫ�ĸ��ʣ�
.�����Ƶ������Ϊ����,���Ƹõ���2017���ͥ���볬��1.5��Ԫ�ĸ��ʣ�
(��)����������,��5��ɽ����ͥ�������볬��2��Ԫ,�����2017���ͥ�����������������,���ж��Ƿ���90%�İ�����Ϊ���õ���2017���ͥ������������йء�?
����![]()
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
����2��Ԫ | ������2��Ԫ | �ܼ� | |
ƽԭ���� | |||
ɽ�� | 5 | ||
�ܼ� |




