题目内容
【题目】已知数列![]() 满足
满足![]() ,
,![]() .
.
(Ⅰ)证明:![]() 是等比数列;
是等比数列;
(Ⅱ)证明:数列![]() 中的任意三项不为等差数列;
中的任意三项不为等差数列;
(Ⅲ)证明:![]() .
.
【答案】(1)证明见解析.
(2)证明见解析.
(3) 证明见解析.
【解析】分析:(Ⅰ)由![]() ,得
,得![]() ,即
,即![]() ,又由
,又由![]() ,所以
,所以![]() 是首项为2,公比为
是首项为2,公比为![]() 的等比数列.
的等比数列.
(Ⅱ)由(1)得数列![]() 的通项公式为
的通项公式为![]() ,不妨设数列
,不妨设数列![]() 中存在三项
中存在三项![]() ,
,![]() ,
,![]() 为等差数列,化简得
为等差数列,化简得![]() ,进而得到
,进而得到![]() ,由于
,由于![]() ,所以上式左边是偶数,右边是奇数,得出矛盾.
,所以上式左边是偶数,右边是奇数,得出矛盾.
(Ⅲ)由(Ⅱ)知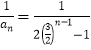 ,则
,则![]() ,
,![]() ,又由当
,又由当![]() 时,化简得到
时,化简得到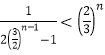 ,即可利用等比数列的求和公式,即可作出证明.
,即可利用等比数列的求和公式,即可作出证明.
详解:(Ⅰ)由![]() ,得
,得![]() ,即
,即![]() ,
,
故![]() .
.
又![]() ,所以
,所以![]() 是首项为2,公比为
是首项为2,公比为![]() 的等比数列.
的等比数列.
(Ⅱ)下面用反证法证明数列![]() 中的任意三项不为等差数列,
中的任意三项不为等差数列,
因为![]() ,因此数列
,因此数列![]() 的通项公式为
的通项公式为![]() .
.
不妨设数列![]() 中存在三项
中存在三项![]() ,
,![]() ,
,![]() 为等差数列,
为等差数列,
又![]() ,
,![]()
![]() ,
,
故![]() ,
,
所以数列![]() 中存在三项为等差数列,只能为
中存在三项为等差数列,只能为![]() 成立.
成立.
即![]()
![]() ,
,
化简为![]() ,
,
两边同乘![]() ,得
,得![]() .
.
又由于![]() ,所以上式左边是偶数,右边是奇数,故上式不成立,导致矛盾.
,所以上式左边是偶数,右边是奇数,故上式不成立,导致矛盾.
(Ⅲ)由(Ⅱ)知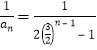 .
.
![]() ,
,![]() ,
,
因为当![]() 时,
时,![]() ,所以
,所以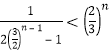 .
.
于是![]()
![]()
![]()
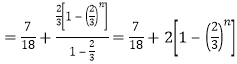
![]() .
.
所以![]() .
.

【题目】为了对2016年某校中考成绩进行分析,在60分以上的全体同学中随机抽出8位,他们的数学分数(已折算为百分制)从小到大排是60、65、70、75、80、85、90、95,物理分数从小到大排是72、77、80、84、88、90、93、95. 参考公式:相关系数  ,
,
回归直线方程是: ![]() ,其中
,其中  ,
,
参考数据: ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(1)若规定85分以上为优秀,求这8位同学中恰有3位同学的数学和物理分数均为优秀的概率;
(2)若这8位同学的数学、物理、化学分数事实上对应如下表:
学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
数学分数x | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 |
物理分数y | 72 | 77 | 80 | 84 | 88 | 90 | 93 | 95 |
化学分数z | 67 | 72 | 76 | 80 | 84 | 87 | 90 | 92 |
①用变量y与x、z与x的相关系数说明物理与数学、化学与数学的相关程度;
②求y与x、z与x的线性回归方程(系数精确到0.01),当某同学的数学成绩为50分时,估计其物理、化学两科的得分.
【题目】某电脑公司有5名产品推销员,其工作年限与年推销金额的数据如表:
推销员编号 | 1 | 2 | 3 | 4 | 5 |
工作年限 | 3 | 5 | 6 | 7 | 9 |
推销金额 | 2 | 3 | 3 | 4 | 5 |
![]() 求年推销金额y关于工作年限x的线性回归方程;
求年推销金额y关于工作年限x的线性回归方程;
![]() 判断变量x与y之间是正相关还是负相关;
判断变量x与y之间是正相关还是负相关;
![]() 若第6名推销员的工作年限是11年,试估计他的年推销金额.
若第6名推销员的工作年限是11年,试估计他的年推销金额.
(参考数据![]() ,
,![]() ,
,
参考公式:线性回归方程![]() 中
中![]() ,
,![]() ,其中
,其中![]() 为样本平均数)
为样本平均数)
