题目内容
7.若关于x的不等式$\sqrt{(x+m)^{2}}$+$\sqrt{(x-1)^{2}}$≤3有解,则实数m的取值范围是[-4,2].分析 $\sqrt{(x+m)^{2}}$+$\sqrt{(x-1)^{2}}$=|x+m|+|x-1|≤3,由绝对值的意义可得|x+m|+|x-1|≤的最小值等于|m+1|,由题意可得|m+1|≤3,由此解得实数a的取值范围.
解答 解:$\sqrt{(x+m)^{2}}$+$\sqrt{(x-1)^{2}}$=|x+m|+|x-1|≤3,
|x+m|+|x-1|表示数轴上的x对应点到-m和1对应点的距离之和,它的最小值等于|m+1|,
故当|m+1|≤3时,关于x的不等式有解,
解得-4≤m≤2,
故实数a的取值范围为[-4,2]
故答案为:[-4,2].
点评 本题主要考查绝对值的意义,绝对值不等式的解法,属于中档题

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
12.命题“?x0∈∁RQ,x0∈Q”的否定是( )
| A. | ?x0∉∁RQ,x0∈Q | B. | ?x0∈∁RQ,x0∈Q | C. | ?x∉∁RQ,x∉Q | D. | ?x∈∁RQ,x∉Q |
16.某地四月份刮东风的概率是$\frac{8}{30}$,既刮东风又下雨的概率是$\frac{7}{30}$,则该地四月份刮东风的条件下,下雨的概率为( )
| A. | $\frac{8}{30}$ | B. | $\frac{7}{8}$ | C. | $\frac{1}{8}$ | D. | $\frac{7}{30}$ |
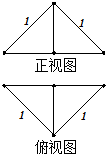 把边长为1的正方形ABCD沿对角线BD折起,形成三棱锥C-ABD,它的正视图与俯视图如图所示,则三棱锥C-ABD的体积为$\frac{\sqrt{2}}{12}$,表面积为1+$\frac{\sqrt{3}}{2}$.
把边长为1的正方形ABCD沿对角线BD折起,形成三棱锥C-ABD,它的正视图与俯视图如图所示,则三棱锥C-ABD的体积为$\frac{\sqrt{2}}{12}$,表面积为1+$\frac{\sqrt{3}}{2}$.