题目内容
已知偶函数f(x),对任意x1,x2∈R,恒有:f(x1+x2)=f(x1)+f(x2)+2x1x2+1,(1)求f(0),f(1),f(2)的值;
(2)求f(x);
(3)判断F(x)=[f(x)]2-2f(x)在(0,+∞)上的单调性.
【答案】分析:(1)直接令x1=x2=0得:f(0)=-1;同样x1=0,x2=1得:f(1)=0;令x1=x2=1得:f(2)=3;
(2)直接根据f[x+(-x)]=f(x)+f(-x)+2x(-x)+1以及f(x)=f(-x),f(0)=-1即可求出f(x);
(3)先求出其解析式,再利用其导函数即可得到在(0,+∞)上的单调性.
解答:解:(1)直接令x1=x2=0得:f(0)=-1,
令x1=1,x2=-1得:f(1-1)=f(1)+f(-1)-2+1=2f(1)-1,∵f(0)=-1∴f(1)=0,
令x1=x2=1得:f(2)=3;
(2)因为:f[x+(-x)]=f(x)+f(-x)+2x(-x)+1,
又f(x)=f(-x),f(0)=-1,
故f(x)=x2-1;
(3)∵F(x)=[f(x)]2-2f(x)=x4-4x2+3,
∴F′(x)=4x3-8x=4x(x2-2)=4x(x+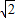 )(x-
)(x-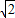 );
);
∴在(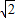 ,+∞)上F′(x)>0,在(0,
,+∞)上F′(x)>0,在(0,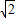 )上F′(x)<0
)上F′(x)<0
故函数F(x)在[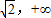 )上是增函数,在(0,
)上是增函数,在(0,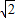 )上为减函数.
)上为减函数.
点评:本题主要考查函数奇偶性与单调性的综合.解决第一问的关键在于赋值法的应用.一般在见到函数解析式不知道而要求具体的函数值时,多用赋值法来解决.
(2)直接根据f[x+(-x)]=f(x)+f(-x)+2x(-x)+1以及f(x)=f(-x),f(0)=-1即可求出f(x);
(3)先求出其解析式,再利用其导函数即可得到在(0,+∞)上的单调性.
解答:解:(1)直接令x1=x2=0得:f(0)=-1,
令x1=1,x2=-1得:f(1-1)=f(1)+f(-1)-2+1=2f(1)-1,∵f(0)=-1∴f(1)=0,
令x1=x2=1得:f(2)=3;
(2)因为:f[x+(-x)]=f(x)+f(-x)+2x(-x)+1,
又f(x)=f(-x),f(0)=-1,
故f(x)=x2-1;
(3)∵F(x)=[f(x)]2-2f(x)=x4-4x2+3,
∴F′(x)=4x3-8x=4x(x2-2)=4x(x+
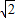 )(x-
)(x-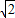 );
);∴在(
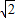 ,+∞)上F′(x)>0,在(0,
,+∞)上F′(x)>0,在(0,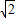 )上F′(x)<0
)上F′(x)<0故函数F(x)在[
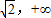 )上是增函数,在(0,
)上是增函数,在(0,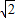 )上为减函数.
)上为减函数.点评:本题主要考查函数奇偶性与单调性的综合.解决第一问的关键在于赋值法的应用.一般在见到函数解析式不知道而要求具体的函数值时,多用赋值法来解决.

练习册系列答案
相关题目