题目内容
13．已知|$\overrightarrow{a}$|=3，|$\overrightarrow{b}$|=2，且3$\overrightarrow{a}$+5$\overrightarrow{b}$与4$\overrightarrow{a}$-3$\overrightarrow{b}$垂直，求$\overrightarrow{a}$与$\overrightarrow{b}$的夹角．分析 利用向量垂直与数量积的关系、向量夹角公式即可得出．
解答 解：∵3$\overrightarrow{a}$+5$\overrightarrow{b}$与4$\overrightarrow{a}$-3$\overrightarrow{b}$垂直，|$\overrightarrow{a}$|=3，|$\overrightarrow{b}$|=2，
∴（3$\overrightarrow{a}$+5$\overrightarrow{b}$）•（4$\overrightarrow{a}$-3$\overrightarrow{b}$）=$12{\overrightarrow{a}}^{2}$+11$\overrightarrow{a}•\overrightarrow{b}$-$15{\overrightarrow{b}}^{2}$=12×32+11×3×2×cosθ-15×22=0，
∴cosθ=$\frac{9}{11}$，
∵θ∈[0，π]，
∴θ=arccos$\frac{9}{11}$．
点评 本题考查了向量垂直与数量积的关系、向量夹角公式，考查了计算能力，属于中档题．
练习册系列答案
小学数学口算题卡脱口而出系列答案
优秀生应用题卡口算天天练系列答案
浙江之星课时优化作业系列答案
相关题目
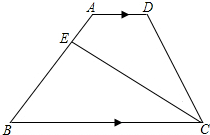如图所示，在梯形ABCD中，BC∥AD，BC=3AD，点E在AB边上，且$\frac{AE}{BE}$=$\frac{1}{4}$，求△BEC的面积与四边形AECD的面积之比．