题目内容
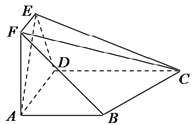
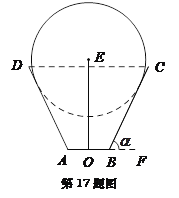
【题目】一儿童游乐场拟建造一个“蛋筒”型游乐设施,其轴截面如图中实线所示. ![]() 是等腰梯形,
是等腰梯形, ![]() 米,
米, ![]() (
(![]() 在
在![]() 的延长线上,
的延长线上, ![]() 为锐角). 圆
为锐角). 圆![]() 与
与![]() 都相切,且其半径长为
都相切,且其半径长为![]() 米.
米. ![]() 是垂直于
是垂直于![]() 的一个立柱,则当
的一个立柱,则当![]() 的值设计为多少时,立柱
的值设计为多少时,立柱![]() 最矮?
最矮?
【答案】当![]() 时,立柱
时,立柱![]() 最矮.
最矮.
【解析】试题分析:利用题意建立直角坐标系,得到关于![]() 的函数:
的函数: ![]() ,求导之后讨论函数的单调性可知
,求导之后讨论函数的单调性可知![]() 时取得最值.
时取得最值.
试题解析:
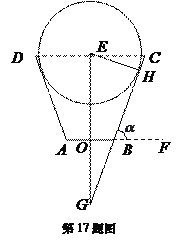
解:方法一:如图所示,以![]() 所在直线为
所在直线为![]() 轴,以线段
轴,以线段
![]() 的垂直平分线为
的垂直平分线为![]() 轴,建立平面直角坐标系.
轴,建立平面直角坐标系.
因为![]() ,
, ![]() ,所以直线
,所以直线![]() 的方程为
的方程为
![]() ,
,
即![]() .
.
设圆心![]() ,由圆
,由圆![]() 与直线
与直线![]() 相切,
相切,
得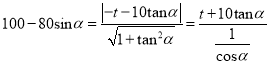 ,
,
所以![]() .
.
令![]() ,
, ![]() ,则
,则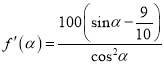 , 设
, 设![]() ,
, ![]() . 列表如下:
. 列表如下:
|
|
|
|
| - | 0 | + |
| 减 | 极小值 | 增 |
所以当![]() ,即
,即![]() 时,
时, ![]() 取最小值. 答:当
取最小值. 答:当![]() 时,立柱
时,立柱![]() 最矮.
最矮.
方法二:如图所示,延长![]() 交于点
交于点![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,
,
则![]() ,
, ![]() .
.
在![]() 中,
中, ![]() . 在
. 在![]() 中,
中, ![]() .
.
所以![]() .
.
(以下同方法一)

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
【题目】某校高三年级共有学生195人,其中女生105人,男生90人.现采用按性别分层抽样的方法,从中抽取13人进行问卷调查.设其中某项问题的选择分别为“同意”、“不同意”两种,且每人都做了一种选择.下面表格中提供了被调查人答卷情况的部分信息.
同意 | 不同意 | 合计 | |
女学生 | 4 | ||
男学生 | 2 |
(Ⅰ)完成上述统计表;
(Ⅱ)根据上表的数据估计高三年级学生该项问题选择“同意”的人数;
(Ⅲ) 从被抽取的女生中随机选取2人进行访谈,求选取的2名女生中至少有一人选择“同意”的概率.