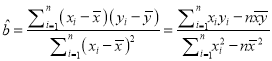题目内容
【题目】设函数![]() .
.
(1)若函数![]() 是奇函数,求实数
是奇函数,求实数![]() 的值;
的值;
(2)若对任意的实数![]() ,函数
,函数![]() (
(![]() 为实常数)的图象与函数
为实常数)的图象与函数![]() 的图象总相切于一个定点.
的图象总相切于一个定点.
① 求![]() 与
与![]() 的值;
的值;
② 对![]() 上的任意实数
上的任意实数![]() ,都有
,都有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)0;(2)①![]() ;②
;②![]() .
.
【解析】试题分析:
(1)由奇函数的 定义得到关于实数a的方程,解方程可得a=0;
(2)由导函数研究函数的 切线可得切点为![]() ,切线的方程为
,切线的方程为![]() ,则
,则![]() .
.
(3)由题意分类讨论 ![]() 和
和![]() 两种情况可得实数
两种情况可得实数![]() 的取值范围是
的取值范围是![]() .
.
试题解析:
解:(1)因为函数![]() 是奇函数,所以
是奇函数,所以![]() 恒成立,
恒成立,
即![]() ,得
,得![]() 恒成立,
恒成立,
![]() .
.
(2)①![]() ,设切点为
,设切点为![]() ,
,
则切线的斜率为![]() ,
,
据题意![]() 是与
是与![]() 无关的常数,故
无关的常数,故![]() ,切点为
,切点为![]() , 由点斜式得切线的方程为
, 由点斜式得切线的方程为![]() ,即
,即![]() ,故
,故![]() .
.
② 当![]() 时,对任意的
时,对任意的![]() ,都有
,都有![]() ;
;
当![]() 时,对任意的
时,对任意的![]() ,都有
,都有![]() ;
;
故![]() 对
对![]() 恒成立,或
恒成立,或![]() 对
对![]() 恒成立.
恒成立.
而![]() ,设函数
,设函数![]() .
.
则![]() 对
对![]() 恒成立,或
恒成立,或![]() 对
对![]() 恒成立,
恒成立, ![]() ,
,
![]() 当
当![]() 时,
时, ![]() ,
,![]() ,
,![]() 恒成立,所以
恒成立,所以![]() 在
在![]() 上递增,
上递增, ![]() ,
,
故![]() 在
在![]() 上恒成立,符合题意.
上恒成立,符合题意. ![]() 当
当![]() 时,令
时,令![]() ,得
,得![]() ,令
,令![]() ,得
,得![]() ,
,
故![]() 在
在![]() 上递减,所以
上递减,所以![]() ,
,
而![]() 设函数
设函数![]() ,
,
则![]() ,
, ![]() 恒成立,
恒成立,
![]() 在
在![]() 上递增,
上递增, ![]() 恒成立,
恒成立,
![]() 在
在![]() 上递增,
上递增, ![]() 恒成立,
恒成立,
即![]() ,而
,而![]() ,不合题意.
,不合题意.
综上![]() ,知实数
,知实数![]() 的取值范围
的取值范围![]() .
.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目