题目内容
【题目】已知圆![]() ,点
,点![]() 为坐标原点,一条直线
为坐标原点,一条直线![]() 与圆
与圆![]() 相切并与椭圆
相切并与椭圆![]() 交于不同的两点
交于不同的两点![]() .
.
(1)设![]() ,求
,求![]() 的表达式;
的表达式;
(2)若![]() ,求直线
,求直线![]() 的方程;
的方程;
(3)若![]() ,求
,求![]() 面积的取值范围.
面积的取值范围.
【答案】(1![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3) .
.
【解析】
(1)利用直线与圆相切可得圆心到直线距离等于半径,求得![]() ;根据直线与椭圆交于不同两点可得
;根据直线与椭圆交于不同两点可得![]() ,求得
,求得![]() ,由此可得
,由此可得![]() ;
;
(2)直线与椭圆方程联立得到韦达定理的形式,利用韦达定理表示出![]() ,由此构造方程求得
,由此构造方程求得![]() ,根据
,根据![]() 可求得
可求得![]() ,进而得到所求直线方程;
,进而得到所求直线方程;
(3)利用![]() 可求得
可求得![]() 的范围;利用弦长公式和点到直线距离公式表示出三角形的底和高,从而将
的范围;利用弦长公式和点到直线距离公式表示出三角形的底和高,从而将![]() 表示为关于
表示为关于![]() 的函数,利用函数值域的求解方法求得结果.
的函数,利用函数值域的求解方法求得结果.
(1)![]() 与圆
与圆![]() 相切,
相切,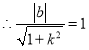 ,则
,则![]() ,
,
由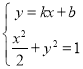 ,消去
,消去![]() 得:
得:![]() ,
,
![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,
,
![]() ,
,![]() ,
,
![]() .
.
(2)设![]() ,
,![]() ,
,
由(1)知:![]() ,
,![]() .
.
则 ![]()
![]() ,
,
解得:![]() ,即
,即![]() ,
,![]() ,
,
![]() 直线
直线![]() 的方程为:
的方程为:![]() 或
或![]() .
.
(3)由(2)知:![]() .
.
![]() ,
,![]() ,解得:
,解得:![]() ,
,
又![]() ,
,
原点![]() 到直线
到直线![]() 距离
距离 ,
,
 ,
,
令![]() ,由
,由![]() 可知:
可知:![]() ,
,![]() ,
,
![]() ,
,
由![]() 得:
得:![]() ,
,![]() ,
,![]() ,
,
即![]() 面积的取值范围为
面积的取值范围为 .
.

【题目】某重点中学高三的一名学生在高考前对他在高三近一年中的所有数学考试(含模拟考试、月考、平时训练等各种类型的试卷)分数进行统计,以此来估计自己在高考中的大致分数.为此,随机抽取了若干份试卷作为样本,根据此样本数据作出如下频率分布统计表和频率分布直方图.
分组 | 频数 | 频率 |
| 20 | 0.25 |
| 50 |
|
|
|
|
| 4 | 0.05 |
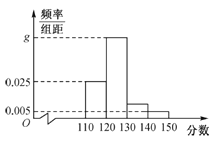
(1)求表中![]() 的值和频率分布直方图中
的值和频率分布直方图中![]() 的值;
的值;
(2)若同组中的每个数据用该组区间的中点值代替,试根据频率分布直方图求该学生高三年级数学考试分数的中位数和平均数,并对该学生自己在高考中的数学成绩进行预测.
【题目】2017年诺贝尔奖陆续揭晓,北京时间10月2日17:30首先公布了生理学和医学奖,获奖者分别是三位美国科学家霍尔(Jeffrey C. Hall)、罗斯巴什(Michael Rosbash)和杨(Michael W. Ymmg),以表彰他们“发现控制生理节律的分子机制”.通过他们的研究成果发现,人类每天睡眠时间在7-9小时为最佳状态.从某大学随机挑选了100名学生(男生、女生各50名)做睡眠时间统计调查,调查结果如下:
睡眠时间(小时) |
|
|
|
|
|
|
|
男生 | 5 | 6 | 12 | 12 | 8 | 5 | 2 |
女生 | 0 | 2 | 6 | 18 | 12 | 10 | 2 |
请根据上面表格回答下列问题:
(1)请分别估计出该校男生和女生的平均睡眠时间;