题目内容
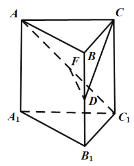
【题目】在棱长均相等的正三棱柱![]() 中,
中,![]() 为
为![]() 的中点,
的中点,![]() 在
在![]() 上,且
上,且![]() ,则下述结论:①
,则下述结论:①![]() ;②
;②![]() ;③平面
;③平面![]() 平面
平面![]() :④异面直线
:④异面直线![]() 与
与![]() 所成角为
所成角为![]() 其中正确命题的个数为( )
其中正确命题的个数为( )
A.1B.2C.3D.4
【答案】B
【解析】
设出棱长,通过直线与直线的垂直判断直线与直线的平行,推出①的正误;判断![]() 是
是![]() 的中点推出②正的误;利用直线与平面垂直推出平面与平面垂直推出③正的误;建立空间直角坐标系求出异面直线
的中点推出②正的误;利用直线与平面垂直推出平面与平面垂直推出③正的误;建立空间直角坐标系求出异面直线![]() 与
与![]() 所成角判断④的正误.
所成角判断④的正误.
解:不妨设棱长为:2,对于①连结![]() ,则
,则![]() ,
,![]() 即
即![]() 与
与![]() 不垂直,又
不垂直,又![]() ,
,![]() ①不正确;
①不正确;
对于②,连结![]() ,
,![]() ,在
,在![]() 中,
中,![]() ,而
,而![]() ,
,![]() 是
是![]() 的中点,所以
的中点,所以![]() ,
,![]() ②正确;
②正确;
对于③由②可知,在![]() 中,
中,![]() ,连结
,连结![]() ,易知
,易知![]() ,而在
,而在![]() 中,
中,![]() ,
,![]() ,
,
即![]() ,又
,又![]() ,
,![]() 面
面![]() ,
,![]() 平面
平面![]() 平面
平面![]() ,
,![]() ③正确;
③正确;
以![]() 为坐标原点,平面
为坐标原点,平面![]() 上过
上过![]() 点垂直于
点垂直于![]() 的直线为
的直线为![]() 轴,
轴,![]() 所在的直线为
所在的直线为![]() 轴,
轴,![]() 所在的直线为
所在的直线为![]() 轴,建立如图所示的直角坐标系;
轴,建立如图所示的直角坐标系;
![]() ,
, ![]() ,
,![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
;
![]() ,
, ![]() ;
;
异面直线![]() 与
与![]() 所成角为
所成角为![]() ,
,![]() ,故
,故![]() .④不正确.
.④不正确.
故选:![]() .
.

练习册系列答案
相关题目
【题目】第十四届全国冬季运动会召开期间,某校举行了“冰上运动知识竞赛”,为了解本次竞赛成绩情况,从中随机抽取部分学生的成绩(得分均为整数,满分100分)进行统计,请根据频率分布表中所提供的数据,解答下列问题:
(1)求![]() 、
、![]() 、
、![]() 的值及随机抽取一考生其成绩不低于70分的概率;
的值及随机抽取一考生其成绩不低于70分的概率;
(2)若从成绩较好的3、4、5组中按分层抽样的方法抽取5人参加“普及冰雪知识”志愿活动,并指定2名负责人,求从第4组抽取的学生中至少有一名是负责人的概率.
组号 | 分组 | 频数 | 频率 |
第1组 |
| 15 | 0.15 |
第2组 |
| 35 | 0.35 |
第3组 |
| b | 0.20 |
第4组 |
| 20 |
|
第5组 |
| 10 | 0.1 |
合计 |
| 1.00 | |