题目内容
(本小题满分15分)如图,过抛物线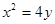 焦点F的直线l与抛物线交于A,B两点(A在第一象限),点C(0,t)(t>1).
焦点F的直线l与抛物线交于A,B两点(A在第一象限),点C(0,t)(t>1).
(I)若△CBF,△CFA,△CBA的面积成等差数列,求直线l的方程;
(II)若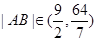 ,且∠FAC为锐角,试求t的取值范围。
,且∠FAC为锐角,试求t的取值范围。
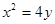 焦点F的直线l与抛物线交于A,B两点(A在第一象限),点C(0,t)(t>1).
焦点F的直线l与抛物线交于A,B两点(A在第一象限),点C(0,t)(t>1).(I)若△CBF,△CFA,△CBA的面积成等差数列,求直线l的方程;
(II)若
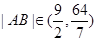 ,且∠FAC为锐角,试求t的取值范围。
,且∠FAC为锐角,试求t的取值范围。

(1)在确定这三个三角形面积时,可转化为同高,这样面积成等差数列,可转化为底|BF|,|FA|,|AB|成等差数列。所以|BF|+|AB|=2|FA|,所以|FA|=2|FB|,可得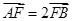 ,这样就转化成基本题型,然后直线方程与抛物线方程联立借助韦达定理解决即可。
,这样就转化成基本题型,然后直线方程与抛物线方程联立借助韦达定理解决即可。
(2)解这个小题应从∠FAC为锐角入手,转化为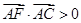 ,再坐标化后,寻找解题途径。
,再坐标化后,寻找解题途径。
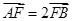 ,这样就转化成基本题型,然后直线方程与抛物线方程联立借助韦达定理解决即可。
,这样就转化成基本题型,然后直线方程与抛物线方程联立借助韦达定理解决即可。(2)解这个小题应从∠FAC为锐角入手,转化为
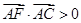 ,再坐标化后,寻找解题途径。
,再坐标化后,寻找解题途径。
练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
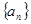 满足
满足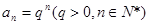 则以下命题中正确的是 。
则以下命题中正确的是 。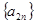 是等比数列 ②
是等比数列 ②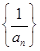 是等比数列
是等比数列 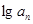 是等差数列 ④
是等差数列 ④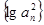 是等差数列
是等差数列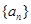 是一个等差数列,且
是一个等差数列,且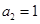 ,
,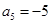 。
。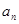 ;
;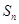 的最大值.
的最大值.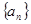 的前n项和
的前n项和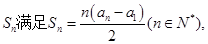 且
且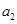 =2.
=2.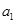 的值,并证明:当n>2时有
的值,并证明:当n>2时有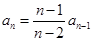 ;
;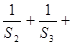 …
…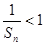 .
.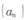 的前n项和为
的前n项和为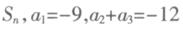 ,则使
,则使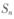 取得最小值时n的值为
取得最小值时n的值为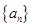 的前
的前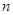 项和为
项和为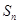 ,且对任意的
,且对任意的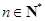 ,都有
,都有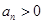 ,
,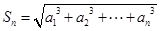 .
.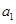 ,
,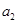 的值;
的值;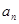
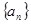 为等差数列,
为等差数列,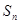 是其前n项的和,且
是其前n项的和,且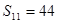 ,则
,则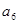 =( )
=( )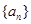 不是常数列,且
不是常数列,且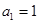 ,若
,若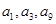 构成等比数列.
构成等比数列.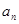 ;
;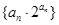 前n项和
前n项和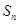
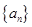 为等差数列,其公差为
为等差数列,其公差为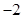 ,且
,且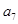 是
是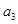 与
与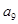 的等比中项,
的等比中项, 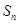 为
为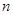 项和,
项和,  ,则
,则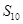 的值为
的值为