题目内容
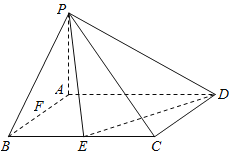
【题目】在四棱锥![]() 中,底面ABCD是矩形,
中,底面ABCD是矩形,![]() 平面ABCD,
平面ABCD,![]() ,E,F是线段BC,AB的中点.
,E,F是线段BC,AB的中点.
![]() Ⅰ
Ⅰ![]() 证明:
证明:![]() ;
;
![]() Ⅱ
Ⅱ![]() 在线段PA上确定点G,使得
在线段PA上确定点G,使得![]() 平面PED,请说明理由.
平面PED,请说明理由.
【答案】(1)见解析(2)见解析
【解析】
(1)由PA⊥平面ABCD先证明DE⊥PA.连接AE,由勾股定理证明DE⊥AE,通过证明DE⊥平面PAE,即可得证PE⊥ED.
(2)过点F作FH∥ED交AD于点H,再过点H作HG∥DP交PA于点G,通过证明平面平面![]() 平面PED,然后证明
平面PED,然后证明![]() 平面PED,.
平面PED,.
解:![]() 1
1![]() 证明:由
证明:由![]() 平面ABCD,得
平面ABCD,得![]() 连接AE,
连接AE,
因为![]() ,
,
所以由勾股定理可得![]() .
.
所以![]() 平面PAE,
平面PAE,
因此![]()
![]() 2
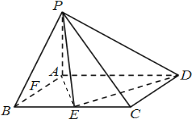
2![]() 过点F作
过点F作![]() 交AD于点H,则
交AD于点H,则![]() 平面PED,且有
平面PED,且有![]() .
.
再过点H作![]() 交PA于点G,则
交PA于点G,则![]() 平面PED,且
平面PED,且![]() .
.
由面面平行的判定定理可得平面![]() 平面PED,
平面PED,
进而由面面平行的性质得到![]() 平面PED,
平面PED,
从而确定G点位置![]()

练习册系列答案
相关题目