题目内容
【题目】设f(x)是定义在R上的增函数,且对于任意的x都有f(﹣x)+f(x)=0恒成立,如果实数a,b满足不等式组 ![]() ,那么a2+b2的取值范围是( )
,那么a2+b2的取值范围是( )
A.[9,49]
B.(17,49]
C.[9,41]
D.(17,41]
【答案】B
【解析】解:∵对于任意的x都有f(﹣x)+f(x)=0恒成立
∴f(﹣x)=﹣f(x)
∵f(a2﹣6a+23)+f(b2﹣8b﹣2)≤0,
∴f(a2﹣6a+23)≤﹣f(2﹣b2+8b),
∵f(x)是定义在R上的增函数,
∴a2﹣6a+23≤2﹣b2+8b,
整理为(a﹣3)2+(b﹣4)2≤4(b>4)
∵(a﹣3)2+(b﹣4)2=4的圆心坐标为:(3,4),半径为2,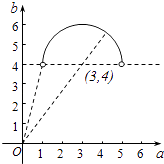
∴(a﹣3)2+(b﹣4)2=4(b>4)内的点到原点距离的取值范围为
( ![]() ,
, ![]() +2],即(
+2],即( ![]() ,7],
,7],
∵a2+b2 表示(a﹣3)2+(b﹣4)2=4内的点到原点距离的平方,
∴a2+b2 的取值范围是(17,49].
故选:B

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目