��Ŀ����
����Ŀ��������{an}��ǰn���ΪSn �� �������������n������an=5Sn+1��������bn= ![]() ��n��N*����
��n��N*����
��1��������{an}������{bn}��ͨ�ʽ��
��2��������{bn}��ǰn���ΪRn �� ��֤���������n��N* �� ����Rn��4n��
��3����cn=b2n��b2n��1��n��N*����������{cn}��ǰn���ΪTn �� ��֤��������n��N* �� ����Tn�� ![]() ��
��
���𰸡�
��1���⣺��an=5Sn+1��
��n=1ʱ��a1=5a1+1����a1=�� ![]() ��
��
��n��2ʱ��an��1=5Sn��1+1��
��an��an��1=5an��
�� ![]() =��
=�� ![]() ��
��
��{an}���ԩ� ![]() Ϊ����ԩ�
Ϊ����ԩ� ![]() Ϊ���ȵĵȱ����У�
Ϊ���ȵĵȱ����У�
��an=���� ![]() ��n��
��n��
��bn= 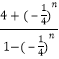 ��
��
��2���⣺�ɣ�1��֪bn= 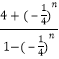 =4+
=4+ ![]() ��
��
��b2k+b2k��1=8+ ![]() +
+ ![]() =8+
=8+ ![]() =8��
=8�� ![]() ��8��
��8��
�൱nΪż��ʱ����n=2m����Rn=��b1+b2��+��b3+b4��+��+��b2m��1+b2m����8m=4n��
��nΪ����ʱ����n=2m��1��Rn=��b1+b2��+��b3+b4��+��+��b2m��3+b2m��2��+b2m��1��8��m��1��+4=4n��
��������n��N*������Rn��4n��
��3���⣺cn=b2n��b2n��1= ![]() +
+ ![]() =
= ![]() =
= ![]() ��
�� ![]() =
= ![]() ��
��
��b1=3��b2= ![]() ����c1=
����c1= ![]() ��
��
�൱n=1ʱ��T1�� ![]() ��
��
��n��2ʱ��Tn�� ![]() +25��
+25�� ![]() +��+
+��+ ![]() ��=
��= ![]() +25��
+25�� 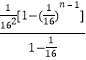
�� ![]() +25��
+25�� ![]() =
= ![]() ��
��
�������n��N*������Tn�� ![]() ��
��
����������1�����ù�ʽan= ![]() ���{an}Ϊ�ȱ����У��ó���ͨ�ʽ������bn=
���{an}Ϊ�ȱ����У��ó���ͨ�ʽ������bn= ![]() �ó�{bn}��ͨ�ʽ����2������bn �� �ó�{bn}����������֮��С��8���Ӷ��ó����ۣ���3������cn �� �ó�cn��
�ó�{bn}��ͨ�ʽ����2������bn �� �ó�{bn}����������֮��С��8���Ӷ��ó����ۣ���3������cn �� �ó�cn�� ![]() ���ӵڶ��ʼʹ�ò���ʽcn��
���ӵڶ��ʼʹ�ò���ʽcn�� ![]() ���ó����ۣ�
���ó����ۣ�
�����㾫����������Ҫ���������е�ǰn��ͺ����е�ͨ�ʽ�����֪ʶ�㣬��Ҫ��������{an}��ǰn���sn��ͨ��an�Ĺ�ϵ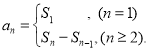 ���������an�ĵ�n����n֮��Ĺ�ϵ������һ����ʽ��ʾ����ô�����ʽ�ͽ�������е�ͨ�ʽ������ȷ�����⣮
���������an�ĵ�n����n֮��Ĺ�ϵ������һ����ʽ��ʾ����ô�����ʽ�ͽ�������е�ͨ�ʽ������ȷ�����⣮

����Ŀ��ij��͵�ÿ�������ס������ֿ�ζ�ĸ�㹲n(nN*)��,ÿ�ݸ��ijɱ�1Ԫ,�ۼ�2Ԫ,�������������,ʣ�µĸ������Ʒ����.����͵귢�������ָ��ÿ�춼��ʣ��,Ϊ�������˹���100�������ָ���������(��λ:��),�õ����µ�ͳ�����ݣ�
���������� | 48 | 49 | 50 | 51 |
���� | 20 | 40 | 20 | 20 |
�ҿ�ζ��������� | 48 | 49 | 50 | 51 |
���� | 40 | 30 | 20 | 10 |
����100���¼�ĸ�������Ƶ����Ϊ�������ĸ���,���������ָ��������������.
(1)�Ǹõ������ָ��ÿ�յ�������ΪX��,��X�ķֲ���
(2)��͵�Ϊ�˼����˷�,��������,��������ÿ���������ķ���
���������˷ѵĸ��ʲ�����0.6,��n�����ֵ;
�������������ָ����������������ֵΪ��������,��ÿ�����Ƹ����ȫ��������n=98֮��ѡ��һ,Ӧѡ�ĸ���
