题目内容
【题目】如图,菱形ABCD的边长为2,△BCD为正三角形,现将△BCD沿BD向上折起,折起后的点C记为C′,且CC′= ![]() ,连接CC′,E为CC′的中点.
,连接CC′,E为CC′的中点. 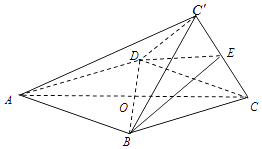
文科:
(1)求证:AC′∥平面BDE;
(2)求证:CC′⊥平面BDE;
(3)求三棱锥C′﹣BCD的体积.
【答案】
(1)证明:连接OE,则在菱形ABCD中,O为AC中点,
又E为CC′的中点,∴OE∥AC′,
∵OE平面BDE,AC′平面BDE,
∴AC′∥平面BDE
(2)证明:由翻折前后可知:
BC=BC′,DC=DC′,
又E为CC′中点,∴BE⊥CC′,DE⊥CC′,
又BE∩DE=E,∴CC′⊥平面BDE
(3)解:连接OE,则由(2)知△CEO为直角三角形,OE⊥BD,
∴BD=2,OE= ![]() ,
,
∴三棱锥C′﹣BCD的体积:
![]()
= ![]()
= ![]()
= ![]()
= ![]() .
.
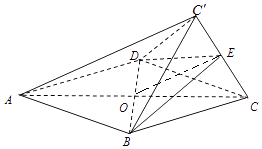
【解析】(1)连接OE,则OE∥AC′,由此能证明AC′∥平面BDE.(2)由翻折前后可知BE⊥CC′,DE⊥CC′,由此能证明CC′⊥平面BDE.(3)连接OE,三棱锥C′﹣BCD的体积: ![]() ,由此能求出结果.
,由此能求出结果.
【考点精析】本题主要考查了直线与平面平行的判定和直线与平面垂直的判定的相关知识点,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想才能正确解答此题.

练习册系列答案
相关题目