题目内容
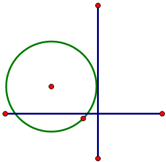
已知圆C经过点A(2,0),B(4,0),C(0,2),
(1)求圆C的方程;
(2)若直线l:y=x+b与圆C有交点,求b的取值范围.
(1)求圆C的方程;
(2)若直线l:y=x+b与圆C有交点,求b的取值范围.
(1)∵圆经过点A(2,0)B(4,0),则圆心在直线x=3上;
设圆心坐标为M(3,b)
则|MA|=|MC|即
=
,
解得b=3,
∴圆C的半径r=|MA|=
,
∴圆C的方程为:(x-3)2+(y-3)2=10;
(2)∵直线l:y=x+b与圆C有交点,
∴圆心M(3,3)到直线l的距离d≤r,即
≤
,
解得-2
≤b≤2
.
∴b的取值范围为[-2
,2
].
设圆心坐标为M(3,b)
则|MA|=|MC|即
| (3-2)2+(b-0)2 |
| (3-0)2+(b-2)2 |
解得b=3,
∴圆C的半径r=|MA|=
| 10 |
∴圆C的方程为:(x-3)2+(y-3)2=10;
(2)∵直线l:y=x+b与圆C有交点,
∴圆心M(3,3)到直线l的距离d≤r,即
| |3-3+b| | ||
|
| 10 |
解得-2
| 5 |
| 5 |
∴b的取值范围为[-2
| 5 |
| 5 |

练习册系列答案
相关题目
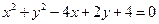 关于直线
关于直线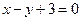 成轴对称的圆的方程是( )
成轴对称的圆的方程是( )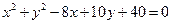
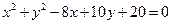
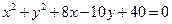
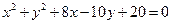
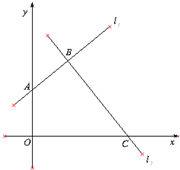
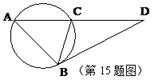
 作圆的切线切于
作圆的切线切于 点,作割线交圆于
点,作割线交圆于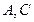 两点,其中
两点,其中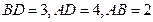 ,则
,则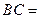 .
.