题目内容
如图,经过B(1,2)作两条互相垂直的直线l1和l2,l1交y轴正半轴于点A,l2交x轴正半轴于点C.
(1)若A(0,1),求点C的坐标;
(2)试问是否总存在经过O,A,B,C四点的圆?若存在,求出半径最小的圆的方程;若不存在,请说明理由.
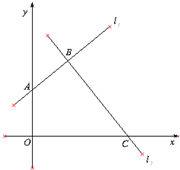
(1)若A(0,1),求点C的坐标;
(2)试问是否总存在经过O,A,B,C四点的圆?若存在,求出半径最小的圆的方程;若不存在,请说明理由.

(1)由直线l1经过两点A(0,1),B(1,2),得l1的方程为x-y+1=0.
由直线l2⊥l1,且直线l2经过点B,得l2的方程为x+y-3=0.
所以,点C的坐标为(3,0).
(2)因为AB⊥BC,OA⊥OC,所以总存在经过O,A,B,C四点的圆,且该圆以AC为直径.
①若l1⊥y轴,则l2∥y轴,此时四边形OABC为矩形,|AC|=
.
②若l1与y轴不垂直,则两条直线斜率都存在.不妨设直线l1的斜率为k,则直线l2的斜率为-
.
所以直线l1的方程为y-2=k(x-1),从而A(0,2-k);
直线l2的方程为y-2=-
(x-1),从而C(2k+1,0).
令
解得k∈(-
,2),注意到k≠0,所以k∈(-
,0)∪(0,2).
此时|AC|2=(2-k)2+(2k+1)2=5k2+5>5,|AC|>
,
所以半径的最小值为
.
此时圆的方程为(x-
)2+(y-1)2=
.
由直线l2⊥l1,且直线l2经过点B,得l2的方程为x+y-3=0.
所以,点C的坐标为(3,0).
(2)因为AB⊥BC,OA⊥OC,所以总存在经过O,A,B,C四点的圆,且该圆以AC为直径.
①若l1⊥y轴,则l2∥y轴,此时四边形OABC为矩形,|AC|=
| 5 |
②若l1与y轴不垂直,则两条直线斜率都存在.不妨设直线l1的斜率为k,则直线l2的斜率为-
| 1 |
| k |
所以直线l1的方程为y-2=k(x-1),从而A(0,2-k);
直线l2的方程为y-2=-
| 1 |
| k |
令
|
| 1 |
| 2 |
| 1 |
| 2 |
此时|AC|2=(2-k)2+(2k+1)2=5k2+5>5,|AC|>
| 5 |
所以半径的最小值为
| ||
| 2 |
此时圆的方程为(x-
| 1 |
| 2 |
| 5 |
| 4 |

练习册系列答案
相关题目
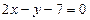 上的圆
上的圆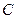 与
与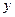 轴交于两点
轴交于两点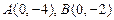 ,则圆
,则圆