题目内容
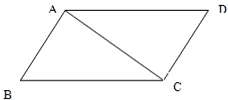
将边长为a的正方形ABCD沿对角线AC折成直二面角,则BD的长度为( )
A.
| B.
| C.
| D.a |
AD=DC=AB=BC=a,
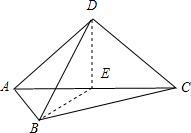
取AC的中点E,连接DE,BE,DE=BE=
a.
∵ABCD是正方形,
∴EB⊥AC,ED⊥AC,
∴∠BED为二面角B-AC-D的平面角,
∴∠BED=90°
∴BD=
=a.
故选:D

取AC的中点E,连接DE,BE,DE=BE=
| ||
| 2 |
∵ABCD是正方形,
∴EB⊥AC,ED⊥AC,
∴∠BED为二面角B-AC-D的平面角,
∴∠BED=90°
∴BD=
| DE2+BE2 |
故选:D

练习册系列答案
相关题目
 的顶点
的顶点 与顶点
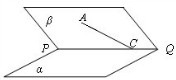
与顶点 分别在平面
分别在平面 的两侧,且梯形的两边
的两侧,且梯形的两边 与
与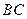 分别与
分别与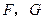 两点;梯形的另两条边
两点;梯形的另两条边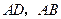 的延长线分别与
的延长线分别与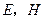 两点,求证:
两点,求证: 四点共线.
四点共线.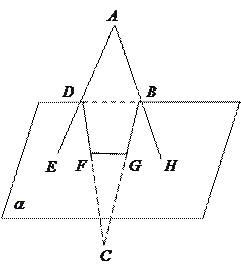
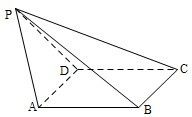
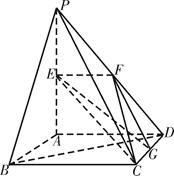 如图,平面
如图,平面 平面ABCD,
平面ABCD,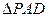 是直角三角形,
是直角三角形, ,E、F、G分别是
,E、F、G分别是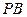 ∥面EFC;
∥面EFC;