题目内容
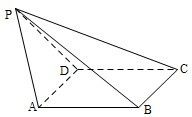
如图,已知四棱锥P-ABCD,PB⊥AD侧面PAD为边长等于2的正三角形,底面ABCD为菱形,侧面PAD与底面ABCD所成的二面角为120°.
(I)求点P到平面ABCD的距离,
(II)求面APB与面CPB所成二面角的大小.
(I)求点P到平面ABCD的距离,
(II)求面APB与面CPB所成二面角的大小.

(I)如图,作PO⊥平面ABCD,垂足为点O.连接OB、OA、OD、OB与AD交于点E,连接PE.
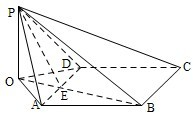
∵AD⊥PB,∴AD⊥OB,
∵PA=PD,∴OA=OD,
于是OB平分AD,点E为AD的中点,所以PE⊥AD.由此知∠PEB为面PAD与面ABCD所成二面角的平面角,
∴∠PEB=120°,∠PEO=60°
由已知可求得PE=
∴PO=PE•sin60°=
×
=
,
即点P到平面ABCD的距离为
.
(II)解法一:如图建立直角坐标系,其中O为坐标原点,x轴平行于DA.P(0,0,
),B(0,
,0),PB中点G的坐标为(0,
,
).连接AG.
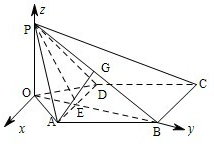
又知A(1,
,0),C(-2,
,0).由此得到:
=(1,-
,-
),
=(0,
,-
),
=(-2,0,0).
于是有
•
=0,
•
=0
所以
⊥
•
⊥
.
,
的夹角θ
等于所求二面角的平面角,
于是cosθ=
=-
,
所以所求二面角的大小为π-arccos
.
解法二:如图,取PB的中点G,PC的中点F,连接EG、AG、GF,则AG⊥PB,FG∥BC,FG=
BC.
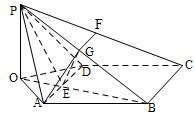
∵AD⊥PB,∴BC⊥PB,FG⊥PB,
∴∠AGF是所求二面角的平面角.
∵AD⊥面POB,∴AD⊥EG.
又∵PE=BE,∴EG⊥PB,且∠PEG=60°.
在Rt△PEG中,EG=PE•cos60°=
.
在Rt△PEG中,EG=
AD=1.
于是tan∠GAE=
=
,
又∠AGF=π-∠GAE.
所以所求二面角的大小为π-arctan
.

∵AD⊥PB,∴AD⊥OB,
∵PA=PD,∴OA=OD,
于是OB平分AD,点E为AD的中点,所以PE⊥AD.由此知∠PEB为面PAD与面ABCD所成二面角的平面角,
∴∠PEB=120°,∠PEO=60°
由已知可求得PE=
| 3 |
∴PO=PE•sin60°=
| 3 |
| ||
| 2 |
| 3 |
| 2 |
即点P到平面ABCD的距离为
| 3 |
| 2 |
(II)解法一:如图建立直角坐标系,其中O为坐标原点,x轴平行于DA.P(0,0,
| 3 |
| 2 |
3
| ||
| 2 |
3
| ||
| 4 |
| 3 |
| 4 |

又知A(1,
| ||
| 2 |
3
| ||
| 2 |
| GA |
| ||
| 4 |
| 3 |
| 4 |
| PB |
3
| ||
| 2 |
| 3 |
| 2 |
| BC |
于是有
| GA |
| PB |
| BC |
| PB |
所以
| GA |
| PB |
| BC |
| PB |
| GA |
| BC |
等于所求二面角的平面角,
于是cosθ=
| ||||
|
|
2
| ||
| 7 |
所以所求二面角的大小为π-arccos
2
| ||
| 7 |
解法二:如图,取PB的中点G,PC的中点F,连接EG、AG、GF,则AG⊥PB,FG∥BC,FG=
| 1 |
| 2 |

∵AD⊥PB,∴BC⊥PB,FG⊥PB,
∴∠AGF是所求二面角的平面角.
∵AD⊥面POB,∴AD⊥EG.
又∵PE=BE,∴EG⊥PB,且∠PEG=60°.
在Rt△PEG中,EG=PE•cos60°=
| ||
| 2 |
在Rt△PEG中,EG=
| 1 |
| 2 |
于是tan∠GAE=
| EG |
| AE |
| ||
| 2 |
又∠AGF=π-∠GAE.
所以所求二面角的大小为π-arctan
| ||
| 2 |

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案
相关题目
 平面
平面 ,求证:过
,求证:过 有且只有一个平面
有且只有一个平面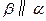 .
.