Question

【题目】已知函数，关于的不等式只有两个整数解，则实数的取值范围是

A. B. C. D.

Answer 1

【答案】C

【解析】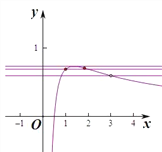

函数f(x)的定义域为(0,+∞)，

则f′(x)= ，

当f′(x)>0得1ln(2x)>0,即ln(2x)<1，

即0<2x<e,即0<x<，

由f′(x)<0得1ln(2x)<0,得ln(2x)>1，

即2x>e,即x>，

即当x=时,函数f(x)取得极大值,同时也是最大值f()==，

即当0<x<时,f(x)< 有一个整数解1，

当x>时,0<f(x)< 有无数个整数解，

若a=0,则+af(x)>0得>0，此时有无数个整数解，不满足条件。

若a>0，

则由+af(x)>0得f(x)>0或f(x)<a，

当f(x)>0时，不等式由无数个整数解，不满足条件。

当a<0时,由+af(x)>0得f(x)>a或f(x)<0，

当f(x)<0时，没有整数解，

则要使当f(x)>a有两个整数解，

∵f(1)=ln2,f(2)= =ln2,f(3)= ，

∴当f(x)ln2时,函数有两个整数点1,2,当f(x) 时，函数有3个整数点1，2，3

∴要使f(x)>a有两个整数解，

则a<ln2，

即ln2<a，

故选C.