题目内容
9.已知函数f(x)=k|x|(x+4)-1.(1)当k>0时,求函数f(x)的单调区间;
(2)若方程f(x)=2至少有三个不相等的实根,求实数k的取值范围.
分析 (1)对x分类,去绝对值,利用二次函数单调性求单调性
(2)根的问题转换为两函数图象交点问题,利用数形结合的方法求解.
解答 解:(1)当x≥0时,f(x)=kx(x+4)-1,
又k>0,
∴(0,+∞)内函数递增;
当x<0时,f(x)=-kx(x+4)-1 k>0
函数增区间为(-∞,-2),减区间为(-2,0).
故函数的增区间为(-∞,-2)和(0,+∞);减区间为(-2,0).
(2)由(1)知当x≥0时最小值为f(0)=-1,当x<0时,f(x)max=f(-2)=4k-1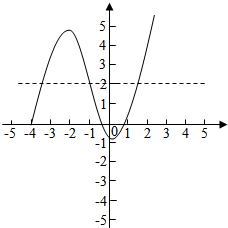
∴4k-1>2,
∴k>$\frac{3}{4}$,
故k的取值范围为k>$\frac{3}{4}$.
点评 考察绝对值函数,分类讨论,转换思想,数形结合等思想.

练习册系列答案
相关题目
18.在△ABC中,内角A,B,C的对边分别为a,b,c,且a=2bsinA,则B=( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{6}$或$\frac{5π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{3}$或$\frac{2π}{3}$ |
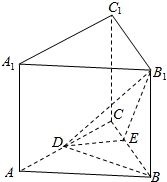 在正三棱柱ABC-A1B1C1中,AB=4,AA1=3,点D是AC的中点,点E在棱BC上(不含端点),且DE⊥B1E.
在正三棱柱ABC-A1B1C1中,AB=4,AA1=3,点D是AC的中点,点E在棱BC上(不含端点),且DE⊥B1E.