题目内容
【题目】某工厂修建一个长方体无盖蓄水池,其容积为6400立方米,深度为4米.池底每平方米的造价为120元,池壁每平方米的造价为100元.设池底长方形的长为x米.
(Ⅰ)求底面积,并用含x的表达式表示池壁面积;
(Ⅱ)怎样设计水池能使总造价最低?最低造价是多少?
【答案】(Ⅰ)底面积1600平方米,池壁面积8(x+![]() )(Ⅱ)当池底设计为边长40米的正方形时,总造价最低,其值为256000元.
)(Ⅱ)当池底设计为边长40米的正方形时,总造价最低,其值为256000元.
【解析】
(1)根据容积,以及深度即可求得底面积;根据底面积,将宽用![]() 表示出来,进而求解出池壁的面积;
表示出来,进而求解出池壁的面积;
(2)根据(1)中所求,建立造价与![]() 之间的函数,用均值不等式求得最小值.
之间的函数,用均值不等式求得最小值.
(Ⅰ)设水池的底面积为S1,池壁面积为S2,
则有![]() (平方米).池底长方形宽为
(平方米).池底长方形宽为![]() 米,
米,
则S2=8x+8×![]() =8(x+
=8(x+![]() ).
).
(Ⅱ)设总造价为y,则
y=120×1 600+100×8![]() ≥192000+64000=256000.
≥192000+64000=256000.
当且仅当x=![]() ,即x=40时取等号.
,即x=40时取等号.
所以x=40时,总造价最低为256000元.
故当池底设计为边长40米的正方形时,总造价最低,其值为256000元.

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的参数方程为
的参数方程为![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为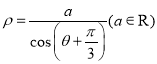 ,直线
,直线![]() 经过椭圆
经过椭圆![]() 的右焦点
的右焦点![]() .
.
(1)求实数![]() 的值;
的值;
(2)设直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,求
两点,求![]() 的值.
的值.
【题目】某高三理科班共有![]() 名同学参加某次考试,从中随机挑出
名同学参加某次考试,从中随机挑出![]() 名同学,他们的数学成绩
名同学,他们的数学成绩![]() 与物理成绩
与物理成绩![]() 如下表:
如下表:
数学成绩 |
|
|
|
|
|
物理成绩 |
|
|
|
|
|
(1)数据表明![]() 与
与![]() 之间有较强的线性关系,求
之间有较强的线性关系,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)本次考试中,规定数学成绩达到![]() 分为优秀,物理成绩达到
分为优秀,物理成绩达到![]() 分为优秀.若该班数学优秀率与物理优秀率分别为
分为优秀.若该班数学优秀率与物理优秀率分别为![]() 和
和![]() ,且除去抽走的
,且除去抽走的![]() 名同学外,剩下的同学中数学优秀但物理不优秀的同学共有
名同学外,剩下的同学中数学优秀但物理不优秀的同学共有![]() 人,请写出
人,请写出![]() 列联表,判断能否在犯错误的概率不超过
列联表,判断能否在犯错误的概率不超过![]() 的前提下认为数学优秀与物理优秀有关?
的前提下认为数学优秀与物理优秀有关?
参考数据: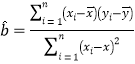 ,
,![]() ;
;![]() ,
,![]() ;
;![]()