题目内容
已知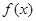 为奇函数,且当
为奇函数,且当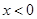 时,
时,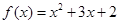 .当
.当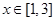 时,
时,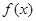 的最大值为
的最大值为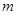 ,最小值为
,最小值为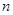 ,求
,求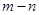 的值.
的值.
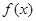 为奇函数,且当
为奇函数,且当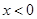 时,
时,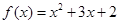 .当
.当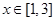 时,
时,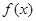 的最大值为
的最大值为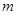 ,最小值为
,最小值为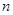 ,求
,求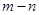 的值.
的值.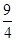 .
.试题分析:要求
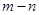 的值,必须求出最大值为
的值,必须求出最大值为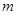 ,最小值为
,最小值为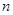 ,一般应该先求出当
,一般应该先求出当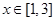 时,
时,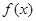 的表达式,而
的表达式,而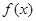 为奇函数,又当
为奇函数,又当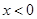 时,
时,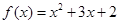 ,故我们可利用奇函数的定义,当
,故我们可利用奇函数的定义,当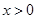 时,
时,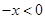 ,
, ,
,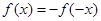 ,故可求出当
,故可求出当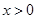 时
时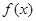 的表达式.
的表达式.试题解析:解 ∵
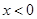 时,
时,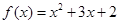 ,且
,且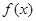 是奇函数,
是奇函数,∴当
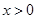 时,
时,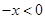 ,则
,则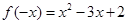 .
.故当
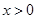 时,
时,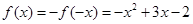 .
.∴当
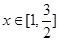 时,
时,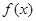 是增函数;
是增函数;当
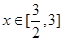 时,
时,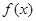 是减函数.
是减函数.因此当
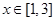 时,
时,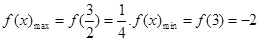 .
.∴
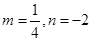 ,从而
,从而 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 其中2<x<6,m为常数,已知销售价格为4元/件时,每月可售出21千件。(1)求m的值; (2)假设该淘宝店员工工资、办公等每月所有开销折合为每件2元(只考虑销售出的件数),试确定销售价格x的值,使该店每月销售饰品所获得的利润最大.(结果保留一位小数)
其中2<x<6,m为常数,已知销售价格为4元/件时,每月可售出21千件。(1)求m的值; (2)假设该淘宝店员工工资、办公等每月所有开销折合为每件2元(只考虑销售出的件数),试确定销售价格x的值,使该店每月销售饰品所获得的利润最大.(结果保留一位小数) 没有零点,则
没有零点,则 的取值范围为 .
的取值范围为 . ,如果对于区间[a,b]中的任意x均有
,如果对于区间[a,b]中的任意x均有 ,则称
,则称 与
与 在区间[a,b]上是“密切函数”,则
在区间[a,b]上是“密切函数”,则 的最大值为 .
的最大值为 .  ,
, )的切线的斜率为
)的切线的斜率为
 的最小值为
的最小值为
 轴有4个交点
轴有4个交点 上为减函数,在
上为减函数,在 上也为减函数
上也为减函数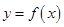 为
为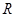 上的可导函数,当
上的可导函数,当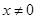 时,
时,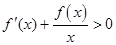 ,则关于
,则关于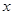 的函数
的函数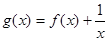 的零点个数为( )
的零点个数为( )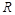 上的函数
上的函数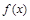 对任意实数
对任意实数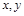 满足
满足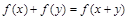 ,且
,且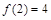 ,则
,则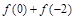 的值为( )
的值为( )