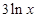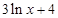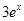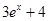题目内容
对于在区间[a,b]上有意义的两个函数 ,如果对于区间[a,b]中的任意x均有
,如果对于区间[a,b]中的任意x均有 ,则称
,则称 在[a,b]上是“密切函数”, [a,b]称为“密切区间”,若函数
在[a,b]上是“密切函数”, [a,b]称为“密切区间”,若函数 与
与 在区间[a,b]上是“密切函数”,则
在区间[a,b]上是“密切函数”,则 的最大值为 .
的最大值为 .
 ,如果对于区间[a,b]中的任意x均有
,如果对于区间[a,b]中的任意x均有 ,则称
,则称 在[a,b]上是“密切函数”, [a,b]称为“密切区间”,若函数
在[a,b]上是“密切函数”, [a,b]称为“密切区间”,若函数 与
与 在区间[a,b]上是“密切函数”,则
在区间[a,b]上是“密切函数”,则 的最大值为 .
的最大值为 . 1
试题分析:由
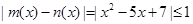 得,
得,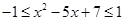 ,这个不等式的解集为
,这个不等式的解集为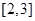 ,由题意得
,由题意得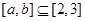 ,所以
,所以 的最大值为
的最大值为 .
. 
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 在区间
在区间 上有最大值4,最小值1,
上有最大值4,最小值1, 的值。
的值。 不等式
不等式 在区间
在区间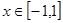 上恒成立,求实数k的取值范围?
上恒成立,求实数k的取值范围?
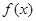 为奇函数,且当
为奇函数,且当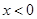 时,
时,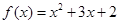 .当
.当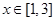 时,
时,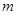 ,最小值为
,最小值为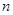 ,求
,求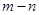 的值.
的值.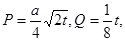 其中
其中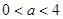 ,今该公司将5亿元投资这两个项目,其中对甲项目投资x(亿元),投资这两个项目所获得的总利润为y(亿元),
,今该公司将5亿元投资这两个项目,其中对甲项目投资x(亿元),投资这两个项目所获得的总利润为y(亿元), ]
] ]
] ]
]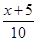 ]
] ,其中
,其中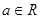 ,若对任意的非零实数
,若对任意的非零实数 ,存在唯一的非零实数
,存在唯一的非零实数 ,使得
,使得 成立,则k的最小值为( )
成立,则k的最小值为( )
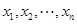 中的最大数为max{
中的最大数为max{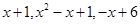 }}= ( )
}}= ( )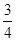
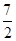
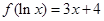 ,则
,则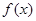 的表达式为( )
的表达式为( )