题目内容
12.若执行如图所示的程序框图后,输出的结果是-29,则判断框中的整数k的值是5.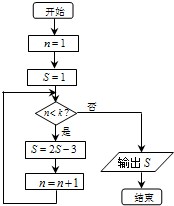
分析 模拟执行程序框图,依次写出每次循环得到的S,n的值,当n=5时应该不满足条件5<k,输出S的值为-29,从而可得判断框中的整数k的值是5.
解答 解:模拟执行程序框图,可得
n=1,S=1
满足条件n<k,S=-1,n=2
满足条件n<k,S=-5,n=3
满足条件n<k,S=-13,n=4
满足条件n<k,S=-29,n=5
由题意,此时应该不满足条件5<k,输出S的值为-29,
则判断框中的整数k的值是5,
故答案为:5.
点评 本题主要考查了循环结构的程序框图,正确判断退出循环的条件是解题的关键,属于基础题.

练习册系列答案
相关题目
2.下列判断不正确的是( )
| A. | 若ξ-B(4,0.25),则Eξ=1 | |
| B. | 命题“?x∈R,x2≥0”的否定是“?x0∈R,x02<0” | |
| C. | 从匀速传递的产品生产线上,检查人员每隔5分钟从中抽出一件产品检查,这样的抽样是系统抽样 | |
| D. | 10名工人某天生产同一零件,生产的件数分别是15,17,14,10,15,17,17,16,14,12,这组数据的中位数与众数相等 |
20.若等式(2x-1)2014=a0+a1x+a2x2+…+a2014x2014对于一切实数x都成立,则a0+$\frac{1}{2}a$1+$\frac{1}{3}$a2+…+$\frac{1}{2015}$a2014=( )
| A. | $\frac{1}{4030}$ | B. | $\frac{1}{2015}$ | C. | $\frac{2}{2015}$ | D. | 0 |
7.某同学用“五点法”画函数f(x)=Asin(ωx+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$)在某一个周期内的图象时,列表并填入的部分数据如表:
(Ⅰ)请求出表中的x1,x2,x3的值,并写出函数f(x)的解析式;
(Ⅱ)将f(x)的图象向右平移$\frac{2}{3}$个单位得到函数g(x)的图象,若函数g(x)在区间[0,m](3<m<4)上的图象的最高点和最低点分别为M,N,求向量$\overrightarrow{NM}$与$\overrightarrow{ON}$夹角θ的大小.
| x | x1 | $\frac{1}{3}$ | x2 | $\frac{7}{3}$ | x3 |
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| Asin(ωx+φ)+B | 0 | $\sqrt{3}$ | 0 | -$\sqrt{3}$ | 0 |
(Ⅱ)将f(x)的图象向右平移$\frac{2}{3}$个单位得到函数g(x)的图象,若函数g(x)在区间[0,m](3<m<4)上的图象的最高点和最低点分别为M,N,求向量$\overrightarrow{NM}$与$\overrightarrow{ON}$夹角θ的大小.
4.函数y=cos2(x+$\frac{π}{2}$)的单调递增区间( )
| A. | (2kπ,2kπ+π)k∈Z | B. | (2kπ,2kπ+2π)k∈Z | C. | (kπ,kπ+$\frac{π}{2}$)k∈Z | D. | (kπ+$\frac{π}{2}$,kπ+π)k∈Z |
1.已知复数z=3+i(i为虚数单位),则z的共轭复数$\overline z$在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
2.已知定义在R上的函数f(x)的导函数为f′(x),满足f′(x)<f(x),f(2)=-2,f(1+x)=-f(1-x),则不等式f(x)<2ex的解集为( )
| A. | (-2,+∞) | B. | (0,+∞) | C. | (1,+∞) | D. | (4,+∞) |