题目内容
18. 如图,在三棱柱ABC-A1B1C1中,AA1⊥面ABC,BC⊥AC,BC=AC=2,D为AC的中点.
如图,在三棱柱ABC-A1B1C1中,AA1⊥面ABC,BC⊥AC,BC=AC=2,D为AC的中点.(1)求证:AB1∥面BDC1;
(2)若二面角A-B1D-A1大小为45°,求直线AC1与平面AB1D所成角的大小.
分析 (1)连结B1C,交BC1于点E,利用中位线定理及线面平行的判定定理即可;
(2)以C为原点,以CC1、CA、CB所在直线分别为x、y、z轴建立空间直角坐标系,利用二面角A-B1D-A1大小为45°,可得确定平面AB1D的法向量与平面A1B1D的法向量,进而可得$\overrightarrow{A{C}_{1}}$与平面AB1D的法向量的夹角,利用互余的关系即得结论.
解答  (1)证明:连结B1C,交BC1于点E,
(1)证明:连结B1C,交BC1于点E,
由题意可得E为B1C的中点,
又∵D为AC的中点,
∴ED∥AB1,
∵ED?平面BDC1,AB1?平面BDC1,
∴AB1∥面BDC1;
(2)解:∵AA1⊥面ABC,BC⊥AC,
∴三棱柱ABC-A1B1C1为直三棱柱,
以C为原点,以CC1、CA、CB所在直线分别为x、y、z轴建立空间直角坐标系如图,
∵BC=AC=2,∴C(0,0,0),A(0,2,0),B(0,0,2),D(0,1,0),
设C1(t,0,0),则A1(t,2,0),B1(t,0,2),
则$\overrightarrow{{B}_{1}D}$=(-t,1,-2),$\overrightarrow{DA}$=(0,1,0),$\overrightarrow{{A}_{1}{B}_{1}}$=(0,-2,2),
设平面AB1D的法向量为$\overrightarrow{m}$=(x1,y1,z1),平面A1B1D的法向量为$\overrightarrow{n}$=(x2,y2,z2),
由$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{{B}_{1}D}=0}\\{\overrightarrow{m}•\overrightarrow{DA}=0}\end{array}\right.$,得$\left\{\begin{array}{l}{-t{x}_{1}+{y}_{1}-2{z}_{1}=0}\\{{y}_{1}=0}\end{array}\right.$,
取x1=2,得$\overrightarrow{m}$=(2,0,-t),
由$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{{B}_{1}D}=0}\\{\overrightarrow{n}•\overrightarrow{{A}_{1}{B}_{1}}=0}\end{array}\right.$,得$\left\{\begin{array}{l}{-t{x}_{2}+{y}_{2}-2{z}_{2}=0}\\{-2{y}_{2}+2{z}_{2}=0}\end{array}\right.$,
取x2=1,得$\overrightarrow{n}$=(1,-t,-t),
∵二面角A-B1D-A1大小为45°,
∴$cos<\overrightarrow{m},\overrightarrow{n}>$=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{{2+t}^{2}}{\sqrt{4+{t}^{2}}•\sqrt{1+2{t}^{2}}}$=cos45°,
解得t=2或-2(舍),
∴C1(2,0,0),$\overrightarrow{A{C}_{1}}$=(2,-2,0),平面AB1D的法向量为$\overrightarrow{m}$=(2,0,-2),
∵$cos<\overrightarrow{m},\overrightarrow{A{C}_{1}}>$=$\frac{\overrightarrow{m}•\overrightarrow{A{C}_{1}}}{|\overrightarrow{m}||\overrightarrow{A{C}_{1}}|}$=$\frac{4}{\sqrt{4+4}•\sqrt{4+4}}$=$\frac{1}{2}$,
∴$\overrightarrow{A{C}_{1}}$与$\overrightarrow{m}$的夹角是$\frac{π}{3}$,
∴所求直线AC1与平面AB1D所成角的大小为$\frac{π}{2}$-$\frac{π}{3}$=$\frac{π}{6}$.
点评 本题考查直线与平面平行的判定,二面角的计算,线面角的计算,考查空间想象能力、计算能力,注意解题方法的积累,属于中档题.

| A. | 甲同学:平均数为2,中位数为2 | B. | 乙同学:中位数为2,唯一的众数为2 | ||
| C. | 丙同学:平均数为2,标准差为2 | D. | 丁同学:平均数为2,唯一的众数为2 |
 将一个半径适当的小球放入如图所示的容器自上方的入口处,小球自由下落,小气在下落的过程中,将遇到黑色障碍物3次,最后落入A袋或B袋中,已知小球每次遇到障碍物时,向左、右两边下落的概率分别是$\frac{1}{3}$,$\frac{2}{3}$
将一个半径适当的小球放入如图所示的容器自上方的入口处,小球自由下落,小气在下落的过程中,将遇到黑色障碍物3次,最后落入A袋或B袋中,已知小球每次遇到障碍物时,向左、右两边下落的概率分别是$\frac{1}{3}$,$\frac{2}{3}$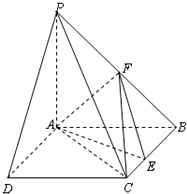 如图所示,PA⊥平面ABCD,ABCD是矩形,AB=1,AD=$\sqrt{3}$,点F是PB的中点,点E在边BC上移动.
如图所示,PA⊥平面ABCD,ABCD是矩形,AB=1,AD=$\sqrt{3}$,点F是PB的中点,点E在边BC上移动. 如图,在△ABC中,CD是∠ACB的平分线,△ACD的外接圆交BC于点E,AB=2AC.
如图,在△ABC中,CD是∠ACB的平分线,△ACD的外接圆交BC于点E,AB=2AC.