Question

3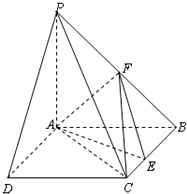．如图所示，PA⊥平面ABCD，ABCD是矩形，AB=1，AD=$\sqrt{3}$，点F是PB的中点，点E在边BC上移动．
（1）证明：PD∥平面AFC；
（2）若PA=1，求证：AF⊥PC；
（3）若二面角P-BC-A的大小为60°，则CE为何值时，三棱锥F-ACE的体积为$\frac{1}{6}$．

Answer 1

分析 （1）连结AC交BD于点Q，连结FQ，利用中位线定理及线面平行的判定定理即得结论；
（2）以A为原点，以AD、AB、AP所在直线分别为x、y、z轴建立空间直角坐标系，通过向量垂直即可说明线段垂直；
（3）通过二面角P-BCV-A的大小为60°求出P点坐标，从而得到F点坐标，根据体积公式计算即可．

解答 （1）证明：连结AC交BD于点Q，连结FQ，
∵四边形ABCD是矩形，∴Q为AC的中点，
又∵点F是PB的中点，∴PD∥FQ，
∴PD∥平面AFC；
（2）证明：以A为原点，以AD、AB、AP所在直线分别为x、y、z轴建立空间直角坐标系如图，
则A（0，0，0），B（0，1，0），C（$\sqrt{3}$，1，0），
∵PA=1，∴P（0，0，1），∴F（0，$\frac{1}{2}$，$\frac{1}{2}$），
∴$\overrightarrow{AF}$=（0，$\frac{1}{2}$，$\frac{1}{2}$），$\overrightarrow{PC}$=（$\sqrt{3}$，1，-1），
∵$\overrightarrow{AF}$•$\overrightarrow{PC}$=（0，$\frac{1}{2}$，$\frac{1}{2}$）•（$\sqrt{3}$，1，-1）=$\frac{1}{2}-\frac{1}{2}$=0，
∴$\overrightarrow{AF}$⊥$\overrightarrow{PC}$，即AF⊥PC；
（3）解：设P（0，0，t），则F（0，$\frac{1}{2}$，$\frac{t}{2}$），
则$\overrightarrow{AP}$=（0，0，t），$\overrightarrow{AF}$=（0，$\frac{1}{2}$，$\frac{t}{2}$），$\overrightarrow{PB}$=（0，1，-t），$\overrightarrow{BC}$=（$\sqrt{3}$，0，0），
设平面PBC的法向量为$\overrightarrow{m}$=（x，y，z），
由$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{BC}=0}\\{\overrightarrow{m}•\overrightarrow{PB}=0}\end{array}\right.$，得$\left\{\begin{array}{l}{\sqrt{3}x=0}\\{y-tz=0}\end{array}\right.$，
令z=1，得$\overrightarrow{m}$=（0，t，1），
∵二面角P-BCV-A的大小为60°，且$\overrightarrow{AP}$是平面ABC的一个法向量，
∴cos60°=$\frac{\overrightarrow{m}•\overrightarrow{AP}}{|\overrightarrow{m}||\overrightarrow{AP}|}$=$\frac{t}{t•\sqrt{1+{t}^{2}}}$=$\frac{1}{2}$，
∴t=1，即$\overrightarrow{AF}$=（0，$\frac{1}{2}$，$\frac{1}{2}$），
设CE=$\sqrt{3}$-x，由三棱锥F-ACE的体积为$\frac{1}{6}$，及V_F-ABE=V_F-ABC-V_F-ACE，
可得$\frac{1}{3}•\frac{1}{2}•1•x•\frac{1}{2}$=$\frac{1}{3}•\frac{1}{2}•1•\sqrt{3}•1$-$\frac{1}{6}$，
解得x=2$\sqrt{3}$-2，∴CE=2-$\sqrt{3}$，
∴CE为2-$\sqrt{3}$时，三棱锥F-ACE的体积为$\frac{1}{6}$．

点评 本题考查直线与平面平行的判定，二面角的计算，棱锥的体积公式，考查空间想象能力、计算能力，注意解题方法的积累，属于中档题．