题目内容
16.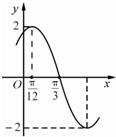 如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π2π2)图象的一部分.
如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π2π2)图象的一部分.(1)求出A,ω,φ的值;
(2)当x∈(0,π2π2)时,求不等式f(x-π6π6)>f2(x2x2-π6π6)-2的解集.
分析 (1)根据三角函数的图象求出A,ω,φ,即可确定函数的解析式;
(2)根据函数的表达式,将不等式进行化简,结合三角函数的单调性进行求解即可.
解答 解:(1)由函数的图象知A=2,T4T4=π3−π12π3−π12=π4π4
∴函数的周期T=π.
即 2πω2πω=π,解得ω=2,
即f(x))=2sin(2x+φ),
由五点对应法得π12π12×2+φ=π2π2,解得φ=π3π3,
∴f(x))=2sin(2x+π3π3).
即A=2,ω=2,φ=π3π3.
(2)由f(x-π6π6)>f2(x2x2-π6π6)-2得2sin2x>4sin2x-2,
即sin2x+cos2x>0,即√2√2sin(2x+π4π4)>0,
∵x∈(0,π2π2),∴2x+π4π4∈(π4π4,5π45π4),
∴π4π4<2x+π4π4<π,
解得0<x<3π83π8,
即不等式的解集为(0,3π83π8).
点评 本题主要考查三角函数解析式的求法以及三角不等式的求解,根据三角函数的图象是解决本题的关键,要求熟练掌握三角函数的图象和性质.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案
相关题目
7.某同学用“五点法”画函数f(x)=Asin(ωx+φ)+B(A>0,ω>0,|φ|<π2π2)在某一个周期内的图象时,列表并填入的部分数据如表:
(Ⅰ)请求出表中的x1,x2,x3的值,并写出函数f(x)的解析式;
(Ⅱ)将f(x)的图象向右平移2323个单位得到函数g(x)的图象,若函数g(x)在区间[0,m](3<m<4)上的图象的最高点和最低点分别为M,N,求向量→NM−−−→NM与→ON−−→ON夹角θ的大小.
| x | x1 | 1313 | x2 | 7373 | x3 |
| ωx+φ | 0 | π2π2 | π | 3π23π2 | 2π |
| Asin(ωx+φ)+B | 0 | √3√3 | 0 | -√3√3 | 0 |
(Ⅱ)将f(x)的图象向右平移2323个单位得到函数g(x)的图象,若函数g(x)在区间[0,m](3<m<4)上的图象的最高点和最低点分别为M,N,求向量→NM−−−→NM与→ON−−→ON夹角θ的大小.
4.函数y=cos2(x+π2π2)的单调递增区间( )
| A. | (2kπ,2kπ+π)k∈Z | B. | (2kπ,2kπ+2π)k∈Z | C. | (kπ,kπ+π2π2)k∈Z | D. | (kπ+π2π2,kπ+π)k∈Z |
1.已知复数z=3+i(i为虚数单位),则z的共轭复数¯z在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
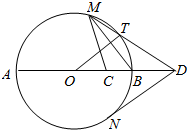 如图,AB是圆O的直径,C是半径OB的中点,D是OB延长线上一点,且BD=OB,直线MD与圆O相交于点M、T(不与A、B重合),DN与圆O相切于点N,连结MC,MB,OT.
如图,AB是圆O的直径,C是半径OB的中点,D是OB延长线上一点,且BD=OB,直线MD与圆O相交于点M、T(不与A、B重合),DN与圆O相切于点N,连结MC,MB,OT.