题目内容
若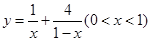 ,则
,则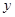 的最小值为 。
的最小值为 。
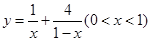 ,则
,则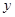 的最小值为 。
的最小值为 。9
试题分析:因为x+(1-x)=1,令1-x=z,x+z=1,
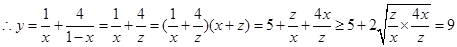 ,当且仅当z=2x,x=
,当且仅当z=2x,x=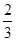 时去的等号,故最小值为9,答案为9.
时去的等号,故最小值为9,答案为9.点评:解决该试题的关键是利用分母中x+(1-x)=1,可以看做和为定值,那么积有最大值的思想来解得。

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
题目内容
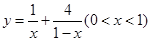 ,则
,则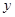 的最小值为 。
的最小值为 。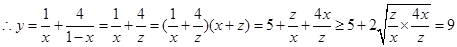 ,当且仅当z=2x,x=
,当且仅当z=2x,x=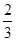 时去的等号,故最小值为9,答案为9.
时去的等号,故最小值为9,答案为9.
 同步练习强化拓展系列答案
同步练习强化拓展系列答案