题目内容
17．
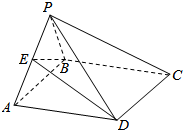如图，在四棱锥P-ABCD中，底面ABCD为平行四边形，平面PAB⊥平面ABCD，且PA=PB，E是PA的中点．（1）求证：PC∥平面EBD；
（2）平面EBD分棱锥P-ABCD为两部分，求这两部分中体积较小者与体积较大者的体积之比．
分析 （1）连接AC，BD，交于O，连接OE，则O是AC的中点，利用三角形中位线的性质，可得OE∥PC，利用线面平行的判定，即可证明结论；
（2）确定VE-ABD=$\frac{1}{4}$VP-ABCD，即可求出这两部分中体积较小者与体积较大者的体积之比．
解答 
（1）证明：连接AC，BD，交于O，连接OE，则O是AC的中点，
∵E是PA的中点，
∴OE∥PC，
∵PC?平面EBD，OE?平面EBD，
∴PC∥平面EBD；
（2）解：由题意，E到平面ABD的距离等于P到平面ABCD的距离的一半，
△ABD的面积是平行四边形ABCD的面积的一半，
∴VE-ABD=$\frac{1}{4}$VP-ABCD，
∴这两部分中体积较小者与体积较大者的体积之比是1：3．
点评 本题考查线面平行，考查体积的计算，正确运用线面平行的判定定理是关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
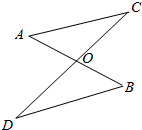如图，线段AB、CD交于点O，且$\frac{AO}{OB}$=$\frac{CO}{OD}$，用向量的运算证明AC∥DB．
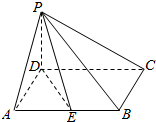已知四棱锥P-ABCD，底面ABCD是菱形，∠DAB=60°，PD⊥平面ABCD，点E为AB中点．
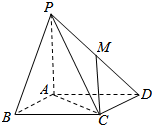如图，在四棱锥P-ABCD中，底面ABCD是边长为1的正方形，PA⊥底面ABCD，PA=AB，点M在棱PD上，PB∥平面ACM．