题目内容
8.(1)设G是△ABC的重心,证明:△GBC,△GAC,△GAB的面积相等.(2)利用(1)的结论,证明:三角形顶点到重心的距离,等于重心到对边中点的距离的2倍.
分析 (1)设三条中线为AD,BE,CF,三中线交于G点,G是重心,由同底等高得到S△GBC=2S△GCD,S△GAC=2S△GCD,由此能证明△GBC,△GAC,△GAB的面积相等.
(2)设三条中线为AD,BE,CF,三中线交于G点,G是重心,由S△GBC=S△GAC,S△GBC=2S△GCD,得到S△GAC=2S△GCD,由此能证明三角形顶点到重心的距离,等于重心到对边中点的距离的2倍.
解答 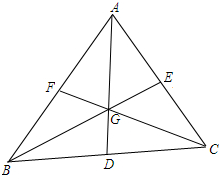 (1)证明:设三条中线为AD,BE,CF,三中线交于G点,G是重心,
(1)证明:设三条中线为AD,BE,CF,三中线交于G点,G是重心,
则AG=2GD,CG=2GF,BG=2GE,
∵BD=CD,∴S△GBC=2S△GCD,
∵AG=2GD,∴S△GAC=2S△GCD,
∴S△GBC=S△GAC,
同理S△GAC=S△GAB,
∴△GBC,△GAC,△GAB的面积相等.
(2)证明:设三条中线为AD,BE,CF,三中线交于G点,G是重心,
∵△GBC,△GAC,△GAB的面积相等,
∴S△GBC=S△GAC,
∵BD=CD,∴S△GBC=2S△GCD,
∴S△GAC=2S△GCD,
∵△AGC和△DGC在分别以AG和DG为底时,高都是点C到边AD的距离,
∴AG=2GD,同理可证CG=2GF,BG=2GE,
∴三角形顶点到重心的距离,等于重心到对边中点的距离的2倍.
点评 本题考查三角形面积相等的证明,考查三角形重心定理的证明,是中档题,解题时要注意三角形面积公式的合理运用.

练习册系列答案
相关题目
18.执行如图所示的程序框图,输出的S的值是( )
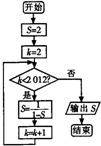

| A. | 2 | B. | -1 | C. | $\frac{1}{2}$ | D. | 1 |
 如图.四棱锥P-ABCD中,PB⊥底面ABCD.PC与平面ABCD所成角的正切值为$\frac{1}{2}$,底面ABCD为直角梯形,AD∥BC,AB⊥BC,AB=AD=PB=3.
如图.四棱锥P-ABCD中,PB⊥底面ABCD.PC与平面ABCD所成角的正切值为$\frac{1}{2}$,底面ABCD为直角梯形,AD∥BC,AB⊥BC,AB=AD=PB=3. 如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,平面PAB⊥平面ABCD,且PA=PB,E是PA的中点.
如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,平面PAB⊥平面ABCD,且PA=PB,E是PA的中点. 如图圆锥的轴截面为等腰直角三角形SAB,Q为底面圆周上一点.
如图圆锥的轴截面为等腰直角三角形SAB,Q为底面圆周上一点.