题目内容
【题目】已知数列{an}的首项a1= ![]() ,an+1=
,an+1= ![]() ,n=1,2,3,….
,n=1,2,3,….
(1)证明:数列{ ![]() ﹣1}是等比数列;
﹣1}是等比数列;
(2)求数列{ ![]() }的前n项和Sn .
}的前n项和Sn .
【答案】
(1)证明:∵ ![]() ,∴
,∴ ![]() ,
,
∴ ![]() ,
,
又 ![]() ,∴
,∴ ![]() ,
,
∴数列 ![]() 是以为
是以为 ![]() 首项,
首项, ![]() 为公比的等比数列.
为公比的等比数列.
(2)解:由(Ⅰ)知 ![]() ﹣1=
﹣1= ![]() ,即
,即 ![]() ,
,
∴ ![]() .
.
设 ![]() …
… ![]() ,①
,①
则 ![]() …
… ![]() ,②
,②
由①﹣②得 ![]() …
… 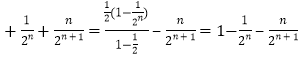 ,
,
∴ ![]() .
.
又1+2+3+… ![]() ,
,
∴数列 ![]() 的前n项和
的前n项和 ![]() .
.
【解析】(1)由an+1= ![]() ,可得
,可得 ![]() ,即可证明数列{
,即可证明数列{ ![]() ﹣1}是等比数列;(2)分组,再利用错位相减法,即可求出数列{
﹣1}是等比数列;(2)分组,再利用错位相减法,即可求出数列{ ![]() }的前n项和Sn .
}的前n项和Sn .
【考点精析】解答此题的关键在于理解等比关系的确定的相关知识,掌握等比数列可以通过定义法、中项法、通项公式法、前n项和法进行判断,以及对数列的前n项和的理解,了解数列{an}的前n项和sn与通项an的关系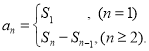 .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目