题目内容
17．若f（x）=（x-a）（x+4）为偶函数，则实数a=4．分析 由题意可得，f（-x）=f（x）对于任意的x都成立，代入整理可得（a-4）x=0对于任意的x都成立，从而可求a
解答 解：∵f（x）=（x-a）（x+4）为偶函数
∴f（-x）=f（x）对于任意的x都成立
即（-x-a）（-x+4）=（x-a）（x+4）
∴x2+（a-4）x-4a=x2+（4-a）x-4a
∴（a-4）x=0
∴a=4
故答案为：4．
点评 本题主要考查了偶函数的定义的应用，属于基础试题
练习册系列答案
华东师大版一课一练系列答案
孟建平名校考卷系列答案
相关题目
7．容量为20的样本数据，分组后的频数如下表：
则样本数据落在区间[40，70）的频率为（ ）
| 分组 | [10，20） | [20，30） | [30，40） | [40，50） | [50，60） | [60，70） |
| 频数 | 2 | 3 | 4 | 5 | 4 | 2 |
| A． | 0.35 | B． | 0.45 | C． | 0.55 | D． | 0.65 |
2．sin70°cos10°+cos110°sin10°=（ ）
| A． | -$\frac{\sqrt{3}}{2}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | -$\frac{1}{2}$ | D． | $\frac{1}{2}$ |
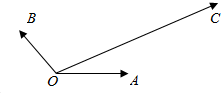如图|$\overrightarrow{OA}|=|\overrightarrow{OB}$|=1，$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为120°，$\overrightarrow{OC}$与$\overrightarrow{OA}$的夹角为30°，|$\overrightarrow{OC}$|=5，则$\overrightarrow{OC}$=$\frac{10\sqrt{3}}{3}$$\overrightarrow{OA}$+$\frac{5\sqrt{3}}{3}$$\overrightarrow{OB}$．（用$\overrightarrow{OA}和\overrightarrow{OB}$表示）