题目内容
9.已知tan α=2,则$\frac{sin2α+cos2(π-α)}{1+cos2α}$的值为$\frac{1}{2}$.分析 利于诱导公式,倍角公式,同角三角函数关系式化简所求后利于已知即可求值.
解答 解:∵tanα=2,
∴$\frac{sin2α+cos2(π-α)}{1+cos2α}$=$\frac{sin2α+cos2α}{1+cos2α}$=$\frac{2sinαcosα+co{s}^{2}α-si{n}^{2}α}{2co{s}^{2}α}$=$\frac{2tanα+1-ta{n}^{2}α}{2}$=$\frac{2×2+1-4}{2}$=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题主要考查了诱导公式,倍角公式,同角三角函数关系式的应用,考查了计算能力,熟练掌握相关公式是解题的关键,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.执行如图所示的程序框图,如果输入m=30,n=18,则输出的m的值为( )


| A. | 0 | B. | 6 | C. | 12 | D. | 18 |
18.已知双曲线C:$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{5}$=1的左、右焦点分别为F1、F2,P为C的右支上一点,且|PF2|=|F1F2|,则cos∠F1F2P等于( )
| A. | $\frac{7}{9}$ | B. | -$\frac{5}{6}$ | C. | -$\frac{7}{18}$ | D. | 1 |
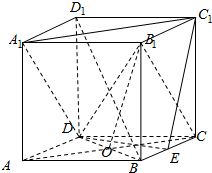 已知正方体ABCD-A1B1C1D1,底面ABCD的中心为O,E为BC的中点,如图
已知正方体ABCD-A1B1C1D1,底面ABCD的中心为O,E为BC的中点,如图