题目内容
6.已知函数f(x)=ex-ax(e为自然对数的底数).(1)当α∈N,且e-2<${∫}_{0}^{1}$f(x)dx<e-1时,求f(x)的最小值;
(2)设不等式f(x)>x的解集为P,且{x|0≤x≤2}⊆P,求实数a的取值范围.
分析 (1)先求的定积分.再解不等式.求出a的值.再判断函数的单调性,从而求f(x)的最小值;
(2)根据不等式f(x)>x的解集为P,且{x|0≤x≤2}⊆P,可转化成,对任意的x∈[0,2],不等式f(x)>x恒成立,将(1+a)x<ex变形为a<$\frac{{e}^{x}}{x}$-1,令(x)=<$\frac{{e}^{x}}{x}$-1,利用导数研究g(x)的最小值,使a小于最小值即可.
解答 解:(1)${∫}_{0}^{1}$f(x)dx=${∫}_{0}^{1}$(ex-ax)dx=(ex-$\frac{1}{2}$ax2)|${\;}_{0}^{1}$=e-$\frac{1}{2}$a-1,
∵e-2<${∫}_{0}^{1}$f(x)dx<e-1,
∴e-2<e-$\frac{1}{2}$a-1<e-1,
∴0<a<2,
∵α∈N,
∴a=1,
∴f(x)=ex-x,
∴f′(x)=ex-1,
∴f(x)在(-∞,0)上是减函数,在[0,+∞)上是增函数,
∴f(x)的最小值为f(0)=1;
(2)∵f(x)=ex-ax,
∴不等式f(x)>x可化为ex-x-ax>0,
又∵不等式f(x)>x的解集为P,且{x|0≤x≤2}⊆P,
由f(x)>x,得(1+a)x<ex
当x=0时,上述不等式显然成立,
故只需考虑x∈(0,2]的情况.
将(1+a)x<ex变形为a<$\frac{{e}^{x}}{x}$-1,
令g(x)=<$\frac{{e}^{x}}{x}$-1,则g′(x)=$\frac{(1-x){e}^{x}}{{x}^{2}}$
令g′(x)>0,解得x>1;令g′(x)<0,解得x<1.
从而g(x)在(0,1)内单调递减,在(1,2)内单调递增.
所以,当x=1时,g(x)取得最小值e-1,从而,
所求实数a的取值范围是(-∞,e-1)
点评 本题主要考查了利用导数求闭区间上函数的最值,以及恒成立问题,一般恒成立求参数问题常常将参数进行分离,转化成研究已知函数在某个区间上的最值问题,考查了划归与转化的思想,属于中档题.

 黄冈创优卷系列答案
黄冈创优卷系列答案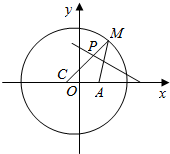 已知圆C:(x+1)2+y2=25,定点A(1,0),M为圆上的一个动点,连接MA,作MA的垂直平分线交半径MC于P,当M点在圆周上运动时,点P的轨迹方程为$\frac{{x}^{2}}{\frac{25}{4}}+\frac{{y}^{2}}{\frac{21}{4}}=1$.
已知圆C:(x+1)2+y2=25,定点A(1,0),M为圆上的一个动点,连接MA,作MA的垂直平分线交半径MC于P,当M点在圆周上运动时,点P的轨迹方程为$\frac{{x}^{2}}{\frac{25}{4}}+\frac{{y}^{2}}{\frac{21}{4}}=1$. 如图,已知边长为4的正方形ABCD,E是BC边上一动点(与B、C不重合),连结AE,作EF⊥AE交∠BCD的外角平分线于F设BE=x,记f(x)=$\overrightarrow{EC}$•$\overrightarrow{CF}$,则函数f(x)的值域是(0,4],当△ECF面积最大时,|$\overrightarrow{EF}$|=2$\sqrt{5}$.
如图,已知边长为4的正方形ABCD,E是BC边上一动点(与B、C不重合),连结AE,作EF⊥AE交∠BCD的外角平分线于F设BE=x,记f(x)=$\overrightarrow{EC}$•$\overrightarrow{CF}$,则函数f(x)的值域是(0,4],当△ECF面积最大时,|$\overrightarrow{EF}$|=2$\sqrt{5}$.