题目内容
1. 如图,已知边长为4的正方形ABCD,E是BC边上一动点(与B、C不重合),连结AE,作EF⊥AE交∠BCD的外角平分线于F设BE=x,记f(x)=$\overrightarrow{EC}$•$\overrightarrow{CF}$,则函数f(x)的值域是(0,4],当△ECF面积最大时,|$\overrightarrow{EF}$|=2$\sqrt{5}$.
如图,已知边长为4的正方形ABCD,E是BC边上一动点(与B、C不重合),连结AE,作EF⊥AE交∠BCD的外角平分线于F设BE=x,记f(x)=$\overrightarrow{EC}$•$\overrightarrow{CF}$,则函数f(x)的值域是(0,4],当△ECF面积最大时,|$\overrightarrow{EF}$|=2$\sqrt{5}$.
分析 可过F作BC的垂线FG,垂足为G,根据条件便知△ABE∽△EGF,可设FG=y,根据相似三角形对应边的比例相等便可得出y=x,从而根据向量数量积的计算公式即可得出f(x)=-(x-2)2+4,从而求该二次函数在(0,4)上的值域即可.根据三角形的面积公式${S}_{△ECF}=\frac{1}{2}(4-x)x$,由基本不等式即可得出x=2时,△ECF面积最大,从而由EF2=EG2+FG2即可得出$|\overrightarrow{EF}|$.
解答 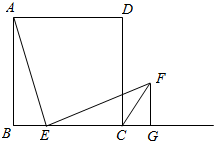 解:如图,作FG⊥BC,交BC延长线于G,根据题意△ABE∽△EGF,设FG=y,则:
解:如图,作FG⊥BC,交BC延长线于G,根据题意△ABE∽△EGF,设FG=y,则:
$\frac{AB}{EG}=\frac{BE}{GF}$;
即$\frac{4}{4-x+y}=\frac{x}{y}$;
∴(4-x+y)x=4y;
∴(4-x)x=(4-x)y;
∵4-x≠0;
∴x=y;
即y=x;
∴$\overrightarrow{EC}•\overrightarrow{CF}=|\overrightarrow{EC}||\overrightarrow{CF}|cos45°$=$(4-x)•\sqrt{2}x•\frac{\sqrt{2}}{2}=(4-x)x$=-x2+4x=-(x-2)2+4;
∴f(x)=-(x-2)2+4,0<x<4;
f(2)=4,f(0)=f(4)=0;
∴0<f(x)≤4;
∴f(x)的值域为(0,4];
${S}_{△ECF}=\frac{1}{2}(4-x)x≤\frac{1}{2}(\frac{4-x+x}{2})^{2}=2$,当4-x=x,即x=2时取“=”;
∴$|\overrightarrow{EF}|=\sqrt{16+4}=2\sqrt{5}$.
故答案为:(0,4],2$\sqrt{5}$.
点评 考查相似三角形的判断,相似三角形的对应边比例关系,二次函数值域求法,根据基本不等式求函数最值,直角三角形的边的关系,向量数量积的计算公式.

 阅读快车系列答案
阅读快车系列答案| A. | [-$\frac{1}{3}$,1] | B. | (-$\frac{1}{3}$,$\frac{1}{3}$) | C. | (-$\frac{1}{3}$,1) | D. | (-∞,-$\frac{1}{3}$) |
